Arbeitsblatt: Test Statistik-Wahrscheinlichkeitsrechnen

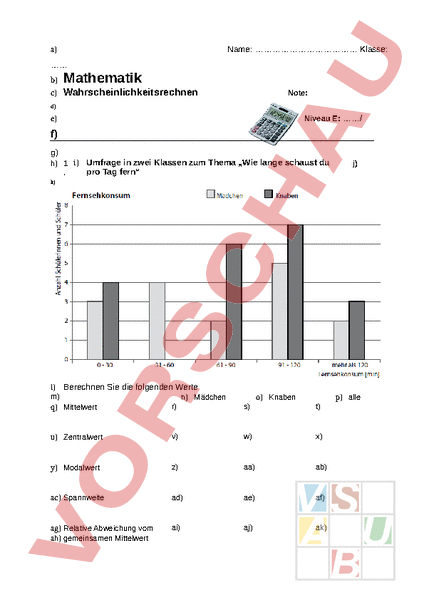
Name: Klasse: a) Mathematik b) c) Wahrscheinlichkeitsrechnen Note: d) Niveau E: / e) f) g) h) 1 i) Umfrage in zwei Klassen zum Thema „Wie lange schaust du pro Tag fern j) k) l) Berechnen Sie die folgenden Werte m) n) Mädchen r) q) Mittelwert o) Knaben p) alle s) t) u) Zentralwert v) w) x) y) Modalwert z) aa) ab) ac) Spannweite ad) ae) af) ag) Relative Abweichung vom ah) gemeinsamen Mittelwert ai) aj) ak) al) Absolute Abweichung vom am) gemeinsamen Mittelwert an) ao) ap) aq) 2 ar) Bestimmen Sie die absolute und relative Häufigkeit der einzelnen Verkehrsteilnehmer bei dieser Verkehrszählung. at) au) av) LKW aw) PKW ax) Busse ay) Motor-räder az) Fahrrad ba) Mofas bb) Fuss-gänger bc) bd) be) bf) bg) bh) bi) bj) Absolute Häufigkeit bk) bl) bm) bn) bo) bp) bq) Relative Häufigkeit br) (%) bs) bt) as) bu) bv) bw) bx) by) bz) ca) 3. cb) Ein Glücksrad wird zweimal gedreht. cc) 1 cd) a) Zeichnen Sie ein Baumdiagramm für zweimaliges Drehen. ce) cf) cg) ch) ci) cj) ck) cl) cm) cn) co) cp) cq) b) Bestimmen Sie die Wahrscheinlichkeit für das Ereignis cr) E1: [zweimal die „1] % c) Bestimmen Sie die Wahrscheinlichkeit für das Ereignis cs) E2: [die zweite Zahl ist größer als die erste] % d) Bestimmen Sie die Wahrscheinlichkeit für das Ereignis ct) E3: [zweimal die selbe Zahl] % cu) cv) 4. cw) Ein Glücksrad ist in 12 gleiche Sektoren unterteilt, die von 1-12 nummeriert sind. Das Glücksrad wird einmal gedreht. Berechnen Sie die Wahrscheinlichkeiten (Bruch und %). cx) cy) a) Mit welcher Wahrscheinlichkeit erhalten wir eine ungerade Zahl? % b) Mit welcher Wahrscheinlichkeit erhalten wir eine Primzahl? % c) Mit welcher Wahrscheinlichkeit erhalten wir eine durch 4 teilbare Zahl? % d) Mit welcher Wahrscheinlichkeit erhalten wir eine Zahl ohne Ziffer 1 oder 2. % cz) da) 5. db) Wir würfeln mit 2 Würfeln und berechnen die Augensumme. Berechen Sie die Wahrscheinlichkeit (Bruch und %). dc) dd) de) a) Wie gross ist die Wahrscheinlichkeit, eine 12 zu würfeln? % b) Wie gross ist die Wahrscheinlichkeit, eine 11 zu würfeln? % c) Wie gross ist die Wahrscheinlichkeit, eine 8 zu würfeln? % d) Wie gross ist die Wahrscheinlichkeit, keine gerade Zahl zu würfeln? % df) 6. dg) In einem Sack sind 7 grüne, 4 blaue und 3 rote Kugeln. Wie gross ist die Wahrscheinlichkeit (Bruch und %), dass man dh) di) a) eine blaue Kugel zieht? % b) eine rote Kugel zieht? % c) keine grüne Kugel zieht? % d) eine grüne oder eine rote Kugel zieht? % dj) 4. dk) Sie ziehen aus folgendem Kartenspiel nacheinander 2 Karten! dl) Berechnen Sie den Erwartungswert Ihres Gewinns. dm) dn) do) Gewinn: Ass: Fr. 5.- Bildkarten (König, Ober, Under, Banner): Fr. 3.- Zahlkarten (6-9): Fr. 0.dp) dq) dr) ds) dt) Gewinn du) dv) dw) dx) dy) dz) ea) Wahrscheinlichkeit eb) (Bruch) ec) ed) ee) ef) eg) eh) ei) ej) Erwartungswert: ek)