Arbeitsblatt: Ganze Zahlen

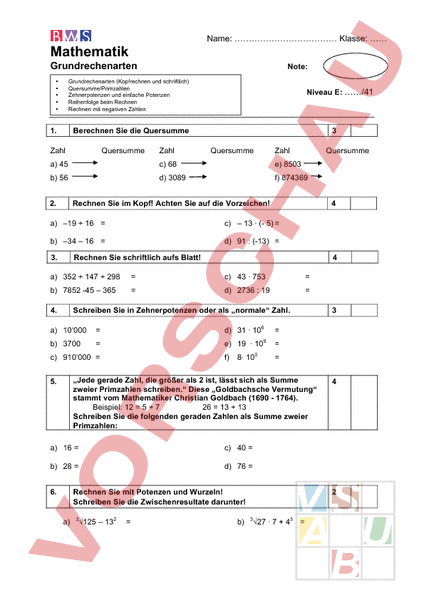
Name: Klasse: Mathematik Grundrechenarten Note: • • • • • • Grundrechenarten (Kopfrechnen und schriftlich) Quersumme/Primzahlen Zehnerpotenzen und einfache Potenzen Reihenfolge beim Rechnen Rechnen mit negativen Zahlen Rechnen mit Potenzen und Wurzeln 1. Berechnen Sie die Quersumme   Zahl Quersumme Zahl Niveau E: /41 3 Quersumme Zahl Quersumme a) 45 c) 68 e) 8503 b) 56 d) 3089 f) 874369 2. Rechnen Sie im Kopf! Achten Sie auf die Vorzeichen! 4 a) –19 16 c) – 13 · (- 5) b) –34 – 16 d) 91 (-13) 3. Rechnen Sie schriftlich aufs Blatt! 4 a) 352 147 298 c) 43 · 753 b) 7852 -45 – 365 d) 2736 19 4. Schreiben Sie in Zehnerpotenzen oder als „normale Zahl. a) 10‘000 d) 31 · 106 b) 3700 e) 19 · 109 8· 100 c) 910‘000 f) „Jede gerade Zahl, die größer als 2 ist, lässt sich als Summe zweier Primzahlen schreiben. Diese „Goldbachsche Vermutung stammt vom Mathematiker Christian Goldbach (1690 1764). Beispiel: 12 5 7 26 13 13 Schreiben Sie die folgenden geraden Zahlen als Summe zweier Primzahlen: 5. a) 16 c) 40 b) 28 d) 76 6. Rechnen Sie mit Potenzen und Wurzeln! Schreiben Sie die Zwischenresultate darunter! a) 3 125 – 132 b) 3 4 2 3 27 · 7 43 7. Beachten Sie beim Berechnen die richtige Reihenfolge der Operationsschritte. Schreiben Sie die Zwischenresultate darunter! a) 60 [ 22 · (32) 6 · 4 c) 25 – 32 – (-34 18) d) b) (23 22 2) 4 · 5 8. b) 110 9 9. 145 143 – 33 9 1091 5–2 592 d) 8 7 10 8 800 4 3 c) 212 12 272 b) 88 ) 4 8 b) 6 10 5–3 b) 16 13 4 5 – 2 Anwendungsaufgaben (Rechnen Sie sauber aufs Blatt!) 2 Setzen Sie die Klammern. Das Resultat soll möglichst klein sein (aber grösser als 0). Schreiben Sie das Resultat dazu. a) 7 5 4 16 12. c) 600 – 200 30 – 5 Setzen Sie Klammern. Das Resultat soll möglichst gross werden. Schreiben Sie das Resultat dazu. a) 16 13 4 11. 4 Bestimmen Sie die fehlenden Zahlen, so dass das Ergebnis stimmt. a) 40 ( 25) 90 10. 5 · 4 · [(3 · 7 – 6) 5 - 1] 17 · 4 Setzen Sie die Klammern, so dass das Ergebnis stimmt. a) 345 – 275 – 5 · 15 4 2 6 a) Die Buskosten für die Schulreise der Klasse 8a kosten jeden der 24 Jugendliche 30Fr. Leider mussten 4 Schüler/innen kurz vor der Fahrt wegen Krankheit absagen. Der Busunternehmer muss aber trotzdem mit dem vollen Preis bezahlt werden. Wie viel muss jetzt jeder mehr bezahlen. b) Roger geht Montag bis Freitag mit seinem Roller in die 12km entfernte Schule. Jeden Mittag isst er zu Hause. Ausser am Mittwoch hat er jeden Nachmittag Unterricht. Auf dem Nachhauseweg, wenn er am Nachmittag Schule hat, geht er noch bei seinem Freund Peter vorbei, was jeweils zusätzlich 3km Fahrt bedeutet. Abends geht er zweimal wöchentlich ins Training ins 4km entfernte Nachbardorf. Wie viele km fährt er so in der Woche? c) Anfangs Mai hat Rebekka 215.- Fr auf ihrem Konto. Nacheinander hat sie 135Fr und 60Fr abgehoben. Ende Monat bekommt sie noch ihren Lohn (500Fr) und bezahlt noch die Haushaltsabgabe an ihre Eltern (125 Fr) und die Handyrechnung (183Fr) und den Krankenkassenbeitrag (246.-) wird vom Konto abgebucht. Wie viel hat sie anfangs Juni noch auf dem Konto?