Arbeitsblatt: Aufgaben zur Pyramide und Kegel

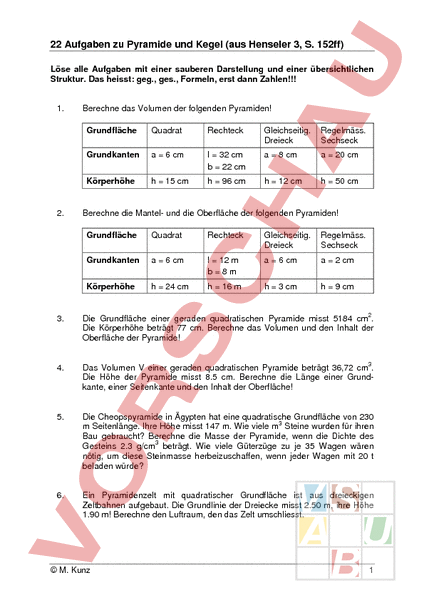
22 Aufgaben zu Pyramide und Kegel (aus Henseler 3, S. 152ff) Löse alle Aufgaben mit einer sauberen Darstellung und einer übersichtlichen Struktur. Das heisst: geg., ges., Formeln, erst dann Zahlen!!! 1. 2. Berechne das Volumen der folgenden Pyramiden! Grundfläche Quadrat Rechteck Gleichseitig. Dreieck Regelmäss. Sechseck Grundkanten 6 cm 32 cm 22 cm 8 cm 20 cm Körperhöhe 15 cm 96 cm 12 cm 50 cm Berechne die Mantel- und die Oberfläche der folgenden Pyramiden! Grundfläche Quadrat Rechteck Gleichseitig. Dreieck Regelmäss. Sechseck Grundkanten 6 cm 12 b8m 6 cm 2 cm Körperhöhe 24 cm 16 3 cm 9 cm 3. Die Grundfläche einer geraden quadratischen Pyramide misst 5184 cm2. Die Körperhöhe beträgt 77 cm. Berechne das Volumen und den Inhalt der Oberfläche der Pyramide! 4. Das Volumen einer geraden quadratischen Pyramide beträgt 36,72 cm3. Die Höhe der Pyramide misst 8.5 cm. Berechne die Länge einer Grundkante, einer Seitenkante und den Inhalt der Oberfläche! 5. Die Cheopspyramide in Ägypten hat eine quadratische Grundfläche von 230 Seitenlänge. Ihre Höhe misst 147 m. Wie viele m3 Steine wurden für ihren Bau gebraucht? Berechne die Masse der Pyramide, wenn die Dichte des Gesteins 2.3 g/cm3 beträgt. Wie viele Güterzüge zu je 35 Wagen wären nötig, um diese Steinmasse herbeizuschaffen, wenn jeder Wagen mit 20 beladen würde? 6. Ein Pyramidenzelt mit quadratischer Grundfläche ist aus dreieckigen Zeltbahnen aufgebaut. Die Grundlinie der Dreiecke misst 2.50 m, ihre Höhe 1.90 m! Berechne den Luftraum, den das Zelt umschliesst. M. Kunz 1 7. Ein Dach hat die Gestalt einer quadratischen Pyramide. Die Seitenkanten messen 6.3 m. Die Seitenhöhe ist 4.8 lang. Wie viele m2 gross ist das Dach? 8. Ein Gedenkstein aus Granit hat die Form einer quadratischen Pyramide. Eine Grundkante misst 2 m, die Höhe ist 5 m. Berechne die Masse des Gedenksteins, wenn die Dichte von Granit 2.7 g/cm3 beträgt! 9. Auf die quadratischen Seitenflächen eines Würfels mit der Kantenlänge 10 cm sind gerade Pyramiden mit der Höhe 5 cm aufgesetzt. a. Wie viele Flächen bilden die Oberfläche des neuen Körpers? b. Um was für Flächen handelt es sich? c. Berechne die Oberfläche! 10. Eine Pyramide mit quadratischer Grundfläche hat ein Volumen von 180 cm3. Eine Grundkante misst 5 cm. Berechne die Länge der Höhe der Pyramide! 11. Berechne das Volumen der folgenden Kegel! 12. 13. Grundkanten Radius Körperhöhe Durchmesser Mantellinie Kegel 1 5 cm 16 cm Kegel 2 20 cm 16 cm Kegel 3 6 cm 10 cm Kegel 4 40 cm 50 cm Berechne die Oberfläche der folgenden Kegel! Grundkanten Radius Körperhöhe Durchmesser Mantellinie Kegel 1 5 cm 16 cm Kegel 2 20 cm 16 cm Kegel 3 6 cm 10 cm Kegel 4 40 cm 50 cm Ein rechtwinkliges Dreieck mit den Katheten 15 cm und 8 cm rotiert um die Kathete a. Berechne den Inhalt der Oberfläche und das Volumen des entstandenen Kegels. M. Kunz 2 14. Ein Sandhaufen hat die Gestalt eines geraden Kreiskegels. Der Durchmesser des Grundkreises misst 6 m, die Länge einer Seitenkante beträgt 9 m. Wie viele Kubikmeter Sand sind dies? 15. Ein Kreissektor hat einen Zentriwinkel von 120. Der Flächeninhalt beträgt 462 m2. Man biegt den Sektor zu einem Kegel. Berechne den Radius der Grundfläche des Kegels! 16. Wie viel Segeltuch, Überlappungen und Verschnitt nicht eingerechnet, sind für den Mantel eines Tipi-Zeltes nötig, wenn das Zelt eine Höhe von 4 und einen Radius von 3 haben soll? 17. Der Achsenschnitt eines geraden Kreiskegels ist ein gleichseitiges Dreieck mit der Seitenlänge 12 cm. Berechne den Inhalt der Oberfläche und das Volumen des Kegels! 18. Ein kegelförmiges Zelt soll 15 m2 Bodenfläche bedecken und eine Höhe von 3.25 haben. Wie viel Stoff braucht es für den Mantel des Kegels? 19. Ein Trichter hat annähernd eine Kegelgestalt. Er ist bis zum Abflussrohr 36 cm tief und hat oben einen Durchmesser von 50 cm Länge. Wie viele Liter fasst er? 20. Ein kegelförmiger Trichter hat oben einen Durchmesser von 20 cm Länge. Wie hoch muss der Trichter sein, wenn er, ohne Ansatzrohr, genau einen Liter fassen soll? 21. Die Fläche eines Quadrates ist gleich gross wie die Mantelfläche eines Kegels. Der Kegel ist 10 cm hoch. Sein Radius misst 5 cm. Berechne den Umfang des Quadrats! 22. Wie viel wiegt ein Kegel aus Tannenholz (Dichte 0.6 g/cm3)? Der Radius der Grundfläche misst 10 cm; die Höhe des Kegels ist 20 cm lang. Viel Erfolg! M. Kunz 3