Arbeitsblatt: Übungsdossier Umfänge und Flächeninhalte berechnen

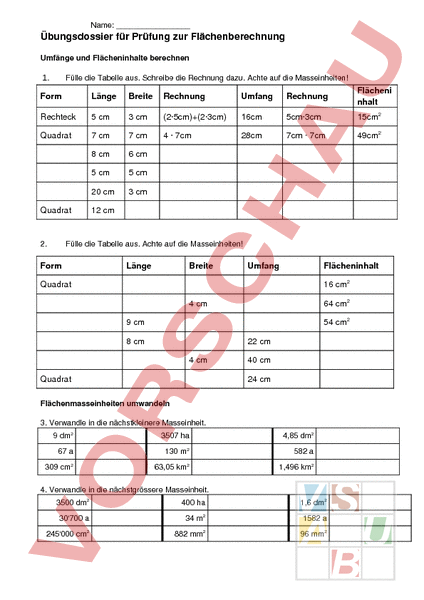
Name: Übungsdossier für Prüfung zur Flächenberechnung Umfänge und Flächeninhalte berechnen 1. Fülle die Tabelle aus. Schreibe die Rechnung dazu. Achte auf die Masseinheiten! Form Länge Breite Rechnung Umfang Rechnung Flächeni nhalt Rechteck 5 cm 3 cm (25cm)(23cm) 16cm 5cm3cm 15cm2 Quadrat 7 cm 7 cm 4 7cm 28cm 7cm 7cm 49cm2 8 cm 6 cm 5 cm 5 cm 20 cm 3 cm Quadrat 2. 12 cm Fülle die Tabelle aus. Achte auf die Masseinheiten! Form Länge Breite Umfang Flächeninhalt 16 cm2 Quadrat 64 cm2 4 cm 54 cm2 9 cm 8 cm 22 cm 4 cm Quadrat 40 cm 24 cm Flächenmasseinheiten umwandeln 3. Verwandle in die nächstkleinere Masseinheit. 9 dm2 3507 ha 4,85 dm2 67 130 m2 582 309 cm2 63,05 km2 1,496 km2 4. Verwandle in die nächstgrössere Masseinheit. 3500 dm2 400 ha 1,6 dm2 30‘700 34 m2 1582 245‘000 cm2 882 mm2 96 mm2 Name: 5. Verwandle in die verlangte Masseinheit. 8 dm2 mm2 85,03 m2 mm2 4,85 km2 23 ha m2 1300 dm2 50082 cm2 m2 30‘900 m2 ha 63‘058 mm2 dm2 0,063 m2 cm2 Rechnen mit Flächenmasseinheiten 6. Berechne die Terme. Achte gut darauf, wo du umrechnen musst! a) 95 cm2 78 cm2 460.20 52 90.45 km2 4500 98 dm2 48.32 m2 b) 6.85 m2 – 4.09 m2 805.39 cm2 – 7.06 dm2 8.26 dm2 – 34 cm 2 79.50 – 30.60 c) 6 89 ha 23 49 dm2 16 3.80 205 1.20 cm2 Satzaufgaben 7. Zwei gleich grosse Quadrate haben eine Seitenlänge von 47 mm. Füge sie zu einem Rechteck zusammen und berechne Umfang und Flächeninhalt des Rechtecks. Wandle den Umfang in Zentimeter um und den Flächeninhalt in Quadratzentimeter. 8. Ein Quadrat hat eine Seitenlänge von 8 cm. Ein Rechteck, das den gleichen Flächeninhalt hat wie das Quadrat, ist 4 cm breit. a) Wie gross ist der Flächeninhalt des Quadrats und des Rechtecks? (Sind ja beide gleich gross!) b) Wie lang ist das Rechteck? 9. Ein Quadrat hat eine Fläche von 49 cm2. Ein Rechteck, das den gleichen Umfang hat wie das Quadrat, ist 10 cm lang. a. Wie gross ist der Umfang des Quadrats oder des Rechtecks? b. Wie breit ist das Rechteck? 10. Ein Papierquadrat mit 40 cm Seitenlänge wird in zwei gleich grosse Rechtecke zerschnitten. Berechne die Fläche eines Solchen Teilrechtecks. 11. Peter zeichnet ein Rechteck mit einer Länge von 10 cm und einer Breite von 1.5 cm. Er ergänzt die Figur so, dass ein Quadrat mit 10 cm Seitenlänge entsteht. Berechne die Fläche der hinzugefügten Figur.