Arbeitsblatt: Würfel anderer Art

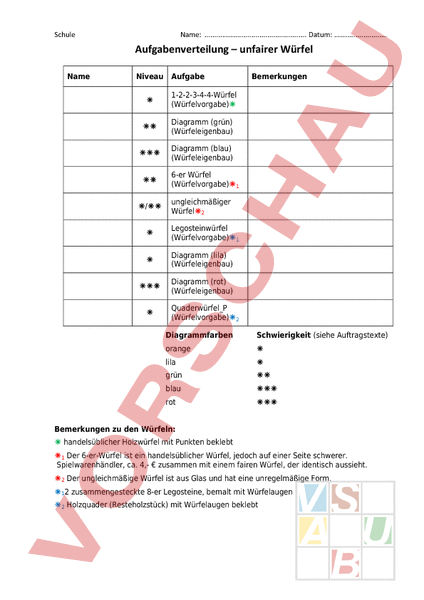
Schule Name: Datum: . Aufgabenverteilung – unfairer Würfel Name Niveau Aufgabe 1-2-2-3-4-4-Würfel (Würfelvorgabe) Diagramm (grün) (Würfeleigenbau) Diagramm (blau) (Würfeleigenbau) / 6-er Würfel (Würfelvorgabe)1 ungleichmäßiger Würfel2 Legosteinwürfel (Würfelvorgabe)1 Diagramm (lila) (Würfeleigenbau) Diagramm (rot) (Würfeleigenbau) Bemerkungen Quaderwürfel_P (Würfelvorgabe)2 Diagrammfarben Schwierigkeit (siehe Auftragstexte) orange lila grün blau rot Bemerkungen zu den Würfeln: handelsüblicher Holzwürfel mit Punkten beklebt 1 Der 6-er-Würfel ist ein handelsüblicher Würfel, jedoch auf einer Seite schwerer. Spielwarenhändler, ca. 4,- € zusammen mit einem fairen Würfel, der identisch aussieht. 2 Der ungleichmäßige Würfel ist aus Glas und hat eine unregelmäßige Form. 12 zusammengesteckte 8-er Legosteine, bemalt mit Würfelaugen 2 Holzquader (Resteholzstück) mit Würfelaugen beklebt Schule Name: Datum: . Würfel anderer Art (unfaire Würfel) Aufgabe 1: Sieh dir deinen Würfel genau an! Schreibe die Würfelpunkte auf, die du auf deinem Würfel vorfindest! . Trage die jeweiligen Würfelpunkte deines Würfels von ihrer Anordnung her in das unten abgebildete Würfelnetz/Quadernetz ein! Tipp: Verwende für die Punkte die gleichen Farben wie auf dem Würfel! Aufgabe 2: Du sollst nun gleich 120 Mal hintereinander Würfeln und nach jedem Wurf deine gewürfelte Zahl durch einen Strich in der Tabelle auf der nächsten Seite versehen! Gib vorher Vermutungen darüber ab, welche Würfelpunktzahl/en du am häufigsten, weniger häufig oder gar nicht würfeln wirst und welche Würfelpunktzahlen etwa gleich oft von dir gewürfelt werden! Schreibe deine Vermutungen hinter die jeweilige Würfelpunktzahl der Tabelle! Würfelpunktzahl meine Vermutungen: Schule Name: Datum: . Begründe deine Vermutung: Aufgabe 3: Jetzt geht es los! Würfele nun insgesamt 120 Mal und führe die Strichliste in der Tabelle! Strichliste Tipp: Mache immer beim 5. Vorkommen einer Würfelpunktzahl einen Schrägstrich! absolute Häufigkeit 120 relative Häufigkeit als Bruch Zähle im Anschluss deine Striche für die einzelnen Würfelpunktzahlen genau aus. Trage deine gezählten Werte (die Anzahl) immer eine Zeile darunter ein! Schreibe dir dein Würfelergebnis hier noch einmal als Ergebnissatz auf! Nach 120 Mal würfeln habe ich . Mal eine Eins gewürfelt, . (Vervollständige den Satz und setze ihn fort!) Schule Name: Datum: . Aufgabe 4: Übertrage nun dein Würfelergebnis in das Koordinatensystem und stelle es als Säulendiagramm dar: Beschrifte (skaliere) die y-Achse mit 5, 10, 15, usw. (von unten Richtung Pfeil)! Markiere danach für jede Würfelpunktzahl mit einem Kreuz die gewürfelten Häufigkeiten (x-Wert Würfelpunktzahl y-Wert Häufigkeit)! Zeichne dann von der x-Achse aus die einzelnen Säulen immer bis zum jeweiligen Punkt nach oben ein! Würfelergebnis, dargestellt als Säulendiagramm absolute Häufigkeiten Aufgabe 5: Betrachte dein Ergebnis und vergleiche es mit deinen anfänglichen Vermutungen! In wie weit hast du recht gehabt oder falsch gelegen? Äußere dich dazu! Schule Name: Datum: . Aufgabe 6: Berechne an dieser Stelle, mit welcher Wahrscheinlichkeit (als Bruch ausgedrückt) die Würfelpunkte 1 bis 6 bei deinem Versuchswürfel gewürfelt werden können: Übertrage dazu von der ersten Seite die Anordnung der Würfelpunkte (zeichne sie nochmals farbig ein)! Übernimm die Farben von oben und färbe im gleichen Verhältnis das folgende Rechteck! Trage hier unten ein, um welchen Bruchteil es sich oben handelt! Addiere die Bruchteile mit gleichen Farben und stelle es in dem folgenden Rechteck dar. Schreibe zu den Farbflächen die berechneten Bruchteile hinzu. Ergänze zum Schluss den Text unten, indem du die Wahrscheinlichkeiten als Bruch angibst! Der 1-2-2-3-4-4-Würfel weist für das Auftreten der unten aufgeführten Ereignisse folgende Wahrscheinlichkeiten auf: (P(E) (Angabe als Bruch)) Es wird eine Eins gewürfelt: P(1) Es wird eine Zwei gewürfelt: P(2) Es wird eine Drei gewürfelt: P(3) Es wird eine Vier gewürfelt: P(4) Es wird eine Fünf gewürfelt: P(5) Es wird eine Sechs gewürfelt: P(6) Schule Name: Datum: . Würfel anderer Art (unfaire Würfel) Aufgabe 1: Sieh dir deinen Würfel genau an! Beschreibe ihn kurz! . . . . . Suche dir von den Schnittvorlagen ein Würfelnetz, das (von der Form her) auf deinen Würfel zutrifft, schneide das Würfelnetz aus und klebe es hier unten ein! [Platz für deine Schnittvorlage] Trage die jeweiligen Würfelpunkte deines Würfels von ihrer Anordnung her in das eingeklebte Würfelnetz ein! Miss jetzt deinen Würfel aus (Länge, Breite, Höhe) und bemaße die 6 verschiedenen Würfelflächen auf dem eingeklebten Würfelnetz! Schule Name: Datum: . Aufgabe 2: Du sollst nun gleich 120 Mal hintereinander Würfeln und nach jedem Wurf deine gewürfelte Zahl durch einen Strich in der Tabelle (auf Seite 3) versehen! Gib vorher Vermutungen darüber ab, welche Würfelpunktzahl/en du am häufigsten, weniger häufig oder eventuell gar nicht würfeln wirst und welche Würfelpunktzahlen etwa gleich oft von dir gewürfelt werden! Schreibe deine Vermutungen hinter die jeweilige Würfelpunktzahl der Tabelle! Würfelpunktzahl meine Vermutungen: Begründe deine Vermutungen: Schule Name: Datum: . Aufgabe 3: Jetzt geht es los! Würfele nun insgesamt 120 Mal und führe die Strichliste in der Tabelle! Strichliste Tipp: Mache immer beim 5. Vorkommen einer Würfelpunktzahl einen Schrägstrich! absolute Häufigkeit relative Häufigkeit als Bruch 120 120 120 120 120 120 120 Zähle im Anschluss deine Striche für die einzelnen Würfelpunktzahlen genau aus. Trage deine gezählten Werte (die Anzahl) immer eine Zeile darunter ein! Schreibe dir dein Würfelergebnis hier noch einmal als Ergebnissatz auf! Nach 120 Mal würfeln habe ich . Mal eine Eins gewürfelt, . (Vervollständige den Satz und setze ihn fort!) Schule Name: Datum: . Aufgabe 4: Übertrage nun dein Würfelergebnis in das Koordinatensystem und stelle es als Säulendiagramm dar: Markiere danach für jede Würfelpunktzahl mit einem Kreuz die gewürfelten Häufigkeiten (x-Wert Würfelpunktzahl y-Wert Häufigkeit)! Zeichne dann von der x-Achse aus die einzelnen Säulen immer bis zum jeweiligen Punkt nach oben ein! Aufgabe 5: Betrachte dein Ergebnis und vergleiche es mit deinen anfänglichen Vermutungen! In wie weit hast du recht gehabt oder falsch gelegen? Äußere dich dazu! Schule Name: Datum: . Aufgabe 6: Berechne an dieser Stelle, mit welcher Wahrscheinlichkeit (als Bruch ausgedrückt) die Würfelpunkte 1 bis 6 bei deinem Versuchswürfel gewürfelt werden können: Berechne dazu zuerst die Flächengröße der einzelnen Würfelseiten (verwende die Maße auf deinem eingeklebten Würfelnetz)! Addiere anschließend die Flächengrößen Nun kannst du jeweils einen Bruch aus deinen Rechenergebnissen machen: Der Zähler ist jeweils eine Einzelfläche (z.B. die Größe von der Augenzahl 1) Bruch strich Der Nenner ist immer deine berechnete Gesamtfläche! Ergänze zum Schluss den Text unten, indem du die Wahrscheinlichkeiten als Bruch angibst! Es wird eine Eins gewürfelt: P(1) Es wird eine Zwei gewürfelt: P(2) Es wird eine Drei gewürfelt: P(3) Es wird eine Vier gewürfelt: P(4) Es wird eine Fünf gewürfelt: P(5) Es wird eine Sechs gewürfelt: P(6) Schule Name: Datum: . Würfel anderer Art (unfaire Würfel) Aufgabe 1: Betrachte zunächst das Säulendiagramm und beantworte die Fragen bzw. führe die Aufgaben dazu durch! Wie oft wurde bei diesem Zufallsexperiment insgesamt gewürfelt? . Vervollständige die Häufigkeitstabelle, indem du die Werte dem Säulendiagramm entnimmst! Notiere die absoluten Häufigkeiten der einzelnen Würfelaugen! Trage dann die relativen Häufigkeiten in Bruchform in die dafür vorgesehene Zeile ein! Überprüfe anschließend, ob deine Werte stimmen (Einzelwerte addieren)! absolute Häufigkeit 1.000 relative Häufigkeit als Bruch als Dezimalwert Welche Würfelaugen wurden am häufigsten gewürfelt? . Welche weniger oder gar nicht? . Stelle eine Vermutung darüber auf, wie dein Würfel gestaltet sein muss! Tipp: Sieh dir dazu die zur Verfügung stehenden Schnittvorlagen sowie die verschiedenen Füllmöglichkeiten an! Zeichne auf der nächsten Seite das Würfelnetz mit den platzierten Würfelaugen für deinen geplanten Würfel! Du darfst dir auch alternativ eine Würfelschnittvorlage (weiße Papierschnittvorlagenblätter) ausschneiden und sie einkleben! Schule Name: Datum: . [Platz für deine Skizze bzw. die Schnittvorlage] Stelle dir nun deinen Würfel her! Wenn du mit deinem Würfel fertig bist Teste deinen hergestellten Würfel und würfele nun 120 Mal hintereinander. Verzeichne nach jedem Wurf deine gewürfelte Zahl durch einen Strich in der Häufigkeitstabelle! Strichliste Tipp: Mache immer beim 5. Vorkommen einer Würfelpunktzahl einen Schrägstrich! absolute Häufigkeit relative Häufigkeit als Bruch als Dezimalwert Vervollständige nun wieder die Häufigkeitstabelle (auf Seite 2): 120 Schule Name: Datum: . Zähle deine Striche für die einzelnen Würfelpunktzahlen genau aus. Trage deine gezählten Werte bei den absoluten Häufigkeiten ein! Füge die Werte für die relative Häufigkeit hinzu! Zeichne deine Ergebnisse in das Säulendiagramm (hier unten) ein! Vergleiche dein Ergebnissäulendiagramm mit der Diagrammvorgabe und beurteile danach, in wie fern es sich etwa deckt oder nicht! . . . . . Beantworte am Ende die Frage, ob dir dein Würfel gelungen ist! Falls nicht, was müsstest du bei einem erneuten Bau ändern? (evtl. Skizze) . . Schule Name: Datum: . Schule Name: Datum: . Schule Name: Datum: . Schule Name: Datum: . Schule Name: Datum: . Schule Name: Datum: . . nach den Auswertungen Schule Name: Datum: . Anhang Würfel-Quaderschnittvorlagen Schule Quaderschnittvorlagen Name: Datum: .