Arbeitsblatt: Test reelle Zahlen

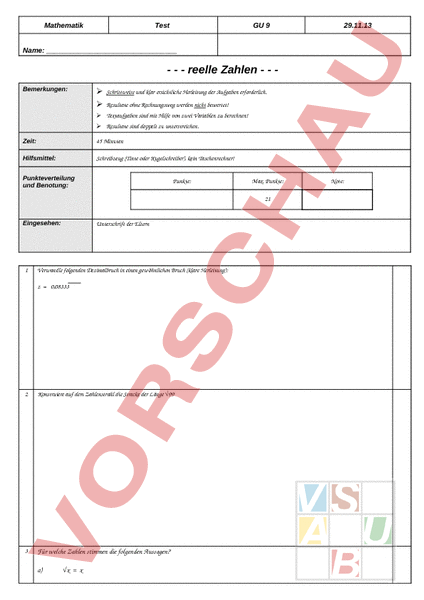
Mathematik Test GU 9 29.11.13 Name: - reelle Zahlen - Bemerkungen: Schrittweise und klar ersichtliche Herleitung der Aufgaben erforderlich. Resultate ohne Rechnungsweg werden nicht bewertet! Textaufgaben sind mit Hilfe von zwei Variablen zu berechnen! Resultate sind doppelt zu unterstreichen. Zeit: 45 Minuten Hilfsmittel: Schreibzeug (Tinte oder Kugelschreiber), kein Taschenrechner! Punkteverteilung und Benotung: Punkte: Max. Punkte: 21 Unterschrift der Eltern Eingesehen: 1 Verwandle folgenden Dezimalbruch in einen gewöhnlichen Bruch (klare Herleitung): 0,08333 2 Konstruiere auf dem Zahlenstrahl die Strecke der Länge 99 3 Für welche Zahlen stimmen die folgenden Aussagen? a) x x Note: 4 b) x · x x c) x x d) x x x a) Nicht jeder Dezimalbruch stellt eine rationale Zahl dar. In welchen Fällen nicht? b) Ist folgender Wurzelwert rational oder irrational? Begründe! 0,04 5 Wodurch unterscheiden sich 36 und 37? Wie heisst die Zahlenmenge Q? Gib zwei Beispiele für diese Zahlenmenge: Welche Grundoperationen sind in uneingeschränkt ausführbar? 6 Wahr oder falsch? Gib zu falschen Aussagen ein Gegenbeispiel? Die Summe von zwei natürlichen Zahlen ist immer natürlich. Die Differenz einer ganzen Zahl und einer irrationalen Zahl ist immer irrational. Das Produkt von zwei irrationalen Zahlen ist immer irrational. Alle nicht abbrechenden, nicht periodischen Dezimalbrüche sind irrational. Zu den reellen Zahlen gehören natürliche Zahlen, rationale Zahlen und irrationale Zahlen. 3 27 45 125 7 Vereinfache und schreibe mit möglichst wenig Wurzeln und keine Wurzeln im Nenner. a) b) 8 Einem Quadrat mit Seitenlänge wird ein gleichseitiges 12 – Eck (rechtwinkliges Kreuz) einbeschrieben. Der Umfang dieses Kreuzes beträgt 36 cm. Berechne den Flächeninhalt dieses Kreuzes und die Länge der Quadratseite s!