Arbeitsblatt: Mathbuch 9 LU 17 Wachstum und Zerfall

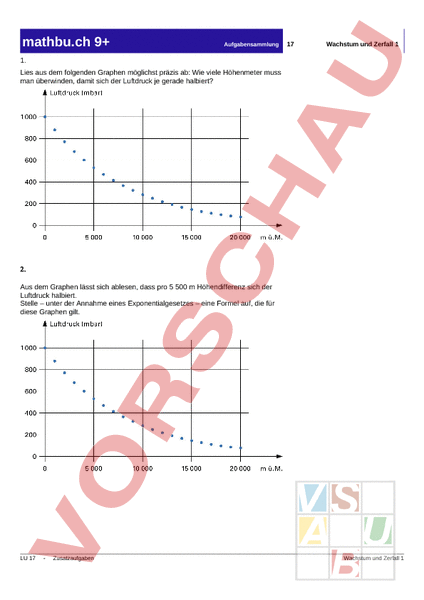
mathbu.ch 9 Aufgabensammlung 17 Wachstum und Zerfall 1 1. Lies aus dem folgenden Graphen möglichst präzis ab: Wie viele Höhenmeter muss man überwinden, damit sich der Luftdruck je gerade halbiert? 2. Aus dem Graphen lässt sich ablesen, dass pro 5 500 Höhendifferenz sich der Luftdruck halbiert. Stelle – unter der Annahme eines Exponentialgesetzes – eine Formel auf, die für diese Graphen gilt. LU 17 Zusatzaufgaben Wachstum und Zerfall 1 mathbu.ch 9 Aufgabensammlung 17 Wachstum und Zerfall 1 3. Prüfe nach, ob der untenstehende Graph auf etwa 1 genau ist, sowohl 5 500 durch die Formel 1 000 1 2 wenn die Anzahl ü. M. angibt, aber auch durch die Formel 1 000 0.88h wenn für h die Anzahl km ü. steht. 4. Im Staate T. leben 5 Millionen Colorados und 20 Millionen Bleichgesichter. Die Population der Bleichgesichter nimmt pro Jahr um 1 ab, jene der Colorados jährlich um 1 zu. Wann sind beide Populationen gleich gross? Hinweis: Denke an die Faustregel für die Verdoppelungszeit. 5. Löse die Gleichung 1.05x 1 000 0.95x 4 000 durch Probieren mit dem Taschenrechner. Wenn die Gleichung so interpretiert wird, dass 5 %-iges Wachstum bei einer Anfangsgrösse von 1 000 und eine 5 %-ige Abnahme bei einer Anfangsgrösse von 4 000 zum gleichen Wert führen sollen, hätte die Sache auch recht genau im Kopf gelöst werden können. Erkläre in Worten! LU 17 Zusatzaufgaben Wachstum und Zerfall 1 mathbu.ch 9 Aufgabensammlung 17 Wachstum und Zerfall 1 6. Auf den 1. Januar 2004 nimmt A. bei der Bank eine Hypothek über CHF 400 000.– auf. Konditionen: Festhypothek über 5 Jahre zu 3.25 %, halbjährlich zu entrichten. Ende Jahr müssen zudem jedes Mal CHF 20 000.– von der Schuld zurückbezahlt („amortisiert) werden. Berechne die Beträge, welche jeweils auf den 30. Juni bzw. 31. Dezember des Jahres zu begleichen sind. 7. Vom Material zersetzt sich pro Monat ein Anteil von 12 %. Das heisst: Nach einem Jahr sind noch 88 0.88 vom anfangs vorhandenen Material vorhanden. Wie lange dauert es, bis noch 50 „aktives Material vorhanden ist? 8. 1970 betrug die Bevölkerungszahl Indiens 800 Mio., 1990 bereits 1100 Mio. Um wie viele ist die Zahl im Mittel pro Jahr angewachsen? Welche Verdoppelungszeit ist demnach zu erwarten? Welche Bevölkerungszahl ist – bei Fortsetzung dieses Trends – für das Jahr 2010 zu erwarten? 9. Behauptung: Könnte man einen einzigen Franken während 500 Jahren zu 7 Zins anlegen, wäre das Kapital dann so gross, dass allein die Zinsen mehr als eine Million Franken pro Sekunde brächte! Rechne nach! 10. Angebot 1: Ein Anfangskapital K0 CHF 1 000.– wird jährlich um CHF 100.– aufgestockt. Angebot 2: Das Anfangskapital wird zu 5 angelegt und mit Zins und Zinseszins liegen gelassen. Nach wie vielen Jahren ist das Angebot 2 erstmals vorteilhafter als das Angebot 1? LU 17 Zusatzaufgaben Wachstum und Zerfall 1