Arbeitsblatt: Mathematikprüfung Symmetrien

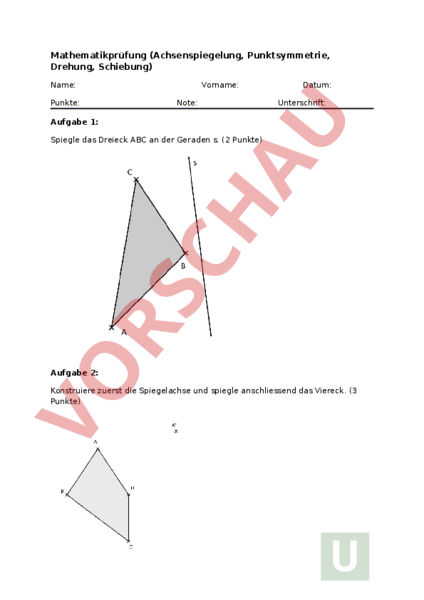
Mathematikprüfung (Achsenspiegelung, Punktsymmetrie, Drehung, Schiebung) Name: Punkte: Vorname: Note: Datum: Unterschrift: Aufgabe 1: Spiegle das Dreieck ABC an der Geraden s. (2 Punkte) Aufgabe 2: Konstruiere zuerst die Spiegelachse und spiegle anschliessend das Viereck. (3 Punkte) Aufgabe 3: a) Zeichne ein Koordinatensystem mit der Einheitsstrecke 1 1 Häuschen. Beschrifte korrekt. (1 Punkt) b) Zeichne das Dreieck ABC mit den Koordinaten A(-5/6), (2/9) und (4/10). (1 Punkt) c) Zeichne die Gerade durch die Punkte (-4/2) und (4/10). (1 Punkt) d) Spiegle das Dreieck an der Geraden g. (1 Punkt) a) b) c) d) e) f) Aufgabe 4: Spiegle die gegebene Figur am Schnittpunkt von EC mit der Mittelsenkrechten AB. (3 Punkte) Aufgabe 5: Zeichne das Dreieck A(1/4), (5/3) und (6/6). Drehe die Figur im Uhrzeigersinn um 100 Grad. Drehpunkt ist im Nullpunkt. Gib die Koordinaten der Bildpunkte an. (4 Punkte) Aufgabe 6: a) Konstruiere ein Parallelogramm mit den Seiten a7cm und b5cm. (1 Punkt) b) Zeichne die Diagonale zwischen und und verlängere diese um 4cm. (1 Punkt) c) Verschiebe das Parallelogramm nun um die Verlängerung der Diagonalen. (2 Punkte) Aufgabe 7: a) Konstruiere ein regelmässiges Dreieck mit der Seitenlänge s4cm. (1 Punkt) b) Konstruiere die Mittelsenkrechte der Strecke und markiere den Schnittpunkt dieser Mittelsenkrechten mit der Parallelen, welche im Abstand von 3cm zu liegt. Dieser Schnittpunkt ist das Drehzentrum. (2 Punkte) c) Drehe das Dreieck nun um 60 Grad im Gegenuhrzeigersinn um das Drehzentrum. (2 Punkte) Aufgabe 8: Spiegle das gegebene Vieleck am Punkt Z. (3 Punkte)