Arbeitsblatt: Einführung Dezimalzahlen

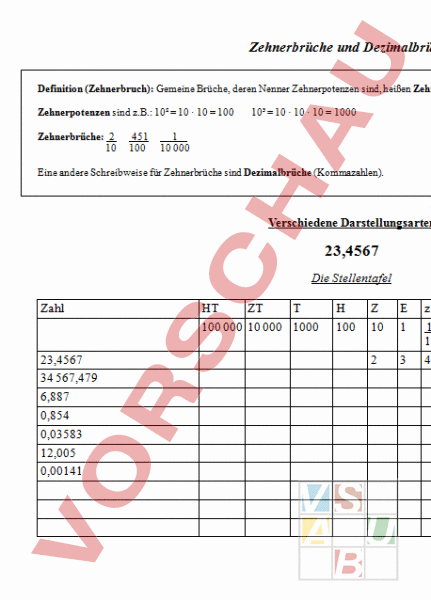
Zehnerbrüche und Dezimalbrüche Definition (Zehnerbruch): Gemeine Brüche, deren Nenner Zehnerpotenzen sind, heißen Zehnerbrüche. Zehnerpotenzen sind z.B.: 10 10 · 10 100 Zehnerbrüche: 2 10 451 100 10 10 · 10 · 10 1000 1 10 000 Eine andere Schreibweise für Zehnerbrüche sind Dezimalbrüche (Kommazahlen). Verschiedene Darstellungsarten 23,4567 Die Stellentafel Zahl HT ZT 100 000 10 000 1000 23,4567 zt ht 100 10 1 1 10 1 100 1 1000 1 10 000 1 100 000 2 3 4 5 6 7 34 567,479 6,887 0,854 0,03583 12,005 0,00141 Copyright 2007 Kerstin Kleist als Summen und gemischte Zahl 23,4567 2Z 3E 4z 5h 6t 7zt 20 3 4 5 6 7 20 3 0,4 0,05 0,006 0,0007 23 4567/10 000 10 100 1000 10 000 Aufgabe 1: Gib die jeweils anderen Darstellungsmöglichkeiten an und trage die Zahl auch in die Stellentafel ein! 1. 456,632 2. 56 753, 5066 3. 6,23456 Aufgabe 2: Welche Zahlen sind es? 1. 200 3000 0,2 40 0,07 6 0,005 2. 9 0,0005 0,7 10 3. 7 60 300 8 5 10 100 0,008 4 0,2 60 0,9 800 3 0,006 40 0,6 9 7000 7 70 100 10 Merke: Bei Dezimalbrüchen dürfen beliebig viele Endnullen angehängt oder weggelassen werden. 0,8 0,80 0,800000, denn man kann den Bruch beliebig mit Zehnerpotenzen erweitern. 8 80 800000 10 100 100 000 Copyright 2007 Kerstin Kleist Die Stellentafel im Dezimalsystem Zehnerbruch HT ZT zt ht Dezimalbruch 34 567 1000 584 667 100 000 4 567 1000 000 345,345 4,5678 0,0547 Dezimalbrüche auf dem Zahlenstrahl Copyright 2007 Kerstin Kleist Vergleichen von Dezimalbrüchen Merke: Wie auch bei den natürlichen Zahlen ist derjenige Bruch kleiner, der auf dem Zahlenstrahl weiter links liegt und somit derjenige der größere, der weiter rechts liegt. Vergleichen mit Hilfe der Stellentafel Zahl 1 ZT Zahl 2 4569,345 4569,367 0,225 0,226 8,024 8,82 3478,016 3478,026 Copyright 2007 Kerstin Kleist