Arbeitsblatt: Grosse Zahlen und Stellenwertsysteme

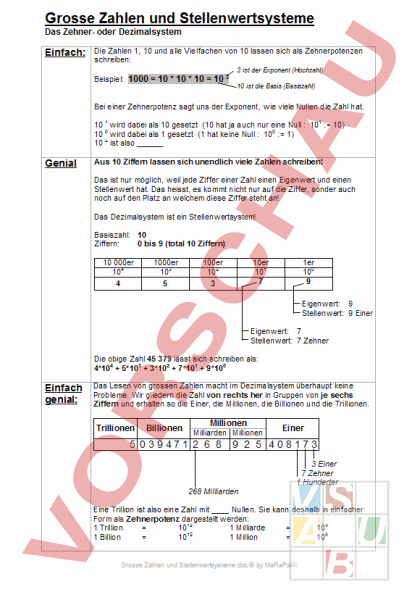
Grosse Zahlen und Stellenwertsysteme Das Zehner- oder Dezimalsystem Einfach: Die Zahlen 1, 10 und alle Vielfachen von 10 lassen sich als Zehnerpotenzen schreiben: 3 ist der Exponent (Hochzahl) Beispiel: 1000 10 10 10 10 3 10 ist die Basis (Basiszahl) Bei einer Zehnerpotenz sagt uns der Exponent, wie viele Nullen die Zahl hat. 10 1 wird dabei als 10 gesetzt (10 hat ja auch nur eine Null 101 : 10) 10 0 wird dabei als 1 gesetzt (1 hat keine Null 100 : 1) 10 2 ist also Aus 10 Ziffern lassen sich unendlich viele Zahlen schreiben! Genial Das ist nur möglich, weil jede Ziffer einer Zahl einen Eigenwert und einen Stellenwert hat. Das heisst, es kommt nicht nur auf die Ziffer, sonder auch noch auf den Platz an welchem diese Ziffer steht an! Das Dezimalsystem ist ein Stellenwertsystem! Basiszahl: 10 Ziffern: 0 bis 9 (total 10 Ziffern) 10 000er 104 4 1000er 103 5 100er 102 3 10er 101 7 1er 100 9 Eigenwert: 9 Stellenwert: 9 Einer Eigenwert: 7 Stellenwert: 7 Zehner Die obige Zahl 45 379 lässt sich schreiben als: 4*104 5*103 3*102 7*101 9*100 Einfach genial: Das Lesen von grossen Zahlen macht im Dezimalsystem überhaupt keine Probleme. Wir gliedern die Zahl von rechts her in Gruppen von je sechs Ziffern und erhalten so die Einer, die Millionen, die Billionen und die Trillionen. Trillionen Billionen Millionen Milliarden Millionen 5 039471 2 6 8 Einer 9 2 5 408173 3 Einer 7 Zehner 1 Hunderter 268 Milliarden Eine Trillion ist also eine Zahl mit Nullen. Sie kann deshalb in einfacher Form als Zehnerpotenz dargestellt werden: 1 Trillion 1018 1 Milliarde 109 1 Billion 1012 1 Million 106 20060906-092535Grosse_Zahlen_und_Stellenwertsysteme_Theorie.doc by MaRaPaWi