Arbeitsblatt: Mathetest 6. Klasse

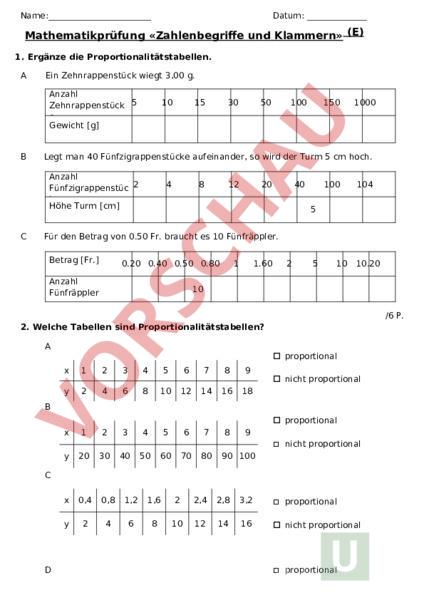
Name: Datum: Mathematikprüfung «Zahlenbegriffe und Klammern» (E) 1. Ergänze die Proportionalitätstabellen. Ein Zehnrappenstück wiegt 3,00 g. Anzahl Zehnrappenstück 5 Gewicht [g] 10 30 50 100 150 1000 Legt man 40 Fünfzigrappenstücke aufeinander, so wird der Turm 5 cm hoch. Anzahl Fünfzigrappenstüc 2 ke Höhe Turm [cm] 15 4 8 12 20 40 100 104 5 Für den Betrag von 0.50 Fr. braucht es 10 Fünfräppler. Betrag [Fr.] 0.20 0.40 0.50 0.80 Anzahl Fünfräppler 1 1.60 2 5 10 10.20 10 /6 P. 2. Welche Tabellen sind Proportionalitätstabellen? proportional 1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 nicht proportional proportional 1 2 3 4 40 5 50 6 60 70 7 80 8 9 nicht proportional proportional 20 30 90 100 0,4 0,8 1,2 1,6 2 2,4 2,8 3,2 2 4 6 8 10 12 14 16 nicht proportional proportional 1,5 3 4,5 6 7,5 9 0,5 1 1,5 2 2,5 3 10,5 12 3,5 nicht proportional 4 proportional y 1 5 3 10 6 15 9 12 20 25 15 30 18 21 35 40 24 nicht proportional proportional 45 x 1 3 6 9 12 15 18 21 24 4 12 24 36 48 60 72 84 96 nicht proportional /6 P. 3. Ergänze die drei Tabellen. Welche sind Proportionalitätstabellen? 1 Liter Benzin kostet an der Tankstelle 1.50 Fr. Anzahl Liter 1 Preis [Fr.] 2 10 20 25 30 40 1.5 Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. Schneidet man eine Schnur in Stücke mit einer Länge von 10 cm, so gibt es 36 Stücke. Wie viele Stücke gibt es jeweils, wenn man die Länge eines Stückes wie folgt wählt? Länge eines Stückes 6 9 10 12 30 40 60 [cm] Anzahl Stücke 36 Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. Mirko sagt eine Zahl. Judith sagt darauf eine Zahl, die jeweils um 5 grösser ist. Mirko sagt: 1 3 5 10 15 50 95 100 Judith sagt: Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. /6,5 P. 4. Übermale alle Quadratzahlen in der untenstehenden Tabelle mit einem roten Farbstift. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 10 1 12 1 14 1 16 1 18 1 20 1 22 1 24 1 26 1 28 1 30 1 32 1 34 1 36 1 38 1 10 2 12 2 14 2 16 2 18 2 20 2 22 2 24 2 26 2 28 2 30 2 32 2 34 2 36 2 38 2 10 3 12 3 14 3 16 3 18 3 20 3 22 3 24 3 26 3 28 3 30 3 32 3 34 3 36 3 38 3 10 4 12 4 14 4 16 4 18 4 20 4 22 4 24 4 26 4 28 4 30 4 32 4 34 4 36 4 38 4 10 5 12 5 14 5 16 5 18 5 20 5 22 5 24 5 26 5 28 5 30 5 32 5 34 5 36 5 38 5 10 6 12 6 14 6 16 6 18 6 20 6 22 6 24 6 26 6 28 6 30 6 32 6 34 6 36 6 38 6 10 7 12 7 14 7 16 7 18 7 20 7 22 7 24 7 26 7 28 7 30 7 32 7 34 7 36 7 38 7 10 8 12 8 14 8 16 8 18 8 20 8 22 8 24 8 26 8 28 8 30 8 32 8 34 8 36 8 38 8 10 9 12 9 14 9 16 9 18 9 20 9 22 9 24 9 26 9 28 9 30 9 32 9 34 9 36 9 38 9 11 0 13 0 15 0 17 0 19 0 21 0 23 0 25 0 27 0 29 0 31 0 33 0 35 0 37 0 39 0 11 1 13 1 15 1 17 1 19 1 21 1 23 1 25 1 27 1 29 1 31 1 33 1 35 1 37 1 39 1 11 2 13 2 15 2 17 2 19 2 21 2 23 2 25 2 27 2 29 2 31 2 33 2 35 2 37 2 39 2 11 3 13 3 15 3 17 3 19 3 21 3 23 3 25 3 27 3 29 3 31 3 33 3 35 3 37 3 39 3 11 4 13 4 15 4 17 4 19 4 21 4 23 4 25 4 27 4 29 4 31 4 33 4 35 4 37 4 39 4 11 5 13 5 15 5 17 5 19 5 21 5 23 5 25 5 27 5 29 5 31 5 33 5 35 5 37 5 39 5 11 6 13 6 15 6 17 6 19 6 21 6 23 6 25 6 27 6 29 6 31 6 33 6 35 6 37 6 39 6 11 7 13 7 15 7 17 7 19 7 21 7 23 7 25 7 27 7 29 7 31 7 33 7 35 7 37 7 39 7 11 8 13 8 15 8 17 8 19 8 21 8 23 8 25 8 27 8 29 8 31 8 33 8 35 8 37 8 39 8 11 9 13 9 15 9 17 9 19 9 21 9 23 9 25 9 27 9 29 9 31 9 33 9 35 9 37 9 39 9 10 0 12 0 14 0 16 0 18 0 20 0 22 0 24 0 26 0 28 0 30 0 32 0 34 0 36 0 38 0 40 0 /5 P. 5. Schreibe die Primfaktorzerlegung folgender Zahlen auf. Schreibe deine Lösung anschliessend auch als Potenzschreibweise auf. Zahlen Primfaktorzerlegung Potenzschreibweis 90 56 46 38 54 72 156 135 265 410 /5 P. 6. Was ist spezielle an einer Primzahl. Erkläre in einem ganzen Satz. /1 P. 7. Schreibe die Rechnung der Zahlenrätsel auf die Linie unter dem entsprechenden Rätsel und die Lösung in das Kästchen am rechten Rand. Addiert man zu einer Zahl den Summanden 16,5 und subtrahiert dann die Zahl 7,2, so erhält man die Differenz 40. Wie lautet die Zahl ? Subtrahiert man 12 von dem Minuenden und multipliziert die Differenz anschliessend mit 14 so erhält man 196. Wie heisst die Zahl x? Ich denke mir eine Zahl und dividiere sie mit dem Dividenden 12. Der Quotient dieser beiden Zahlen wird anschliessend mit dem Faktor 9 verrechnet und von dem entstandenen Ergebnis der Subtrahend 7 abgezogen. Die dadurch entstandene Differenz ist 20. An welche Zahl habe ich gedacht? Die Summe der Zahlen 12 und wird mit dem Minuenden 20 verrechnet und anschliessend durch den Divisor 2 dividiert. Der dadurch entstandene Quotient ist 1. Wie lautet die Zahl x? Die Differenz aus einer Zahl und dem Subtrahenden 8 wird mit dem Produkt des Faktors 6 mit sich selbst addiert. Die daraus entstehende Summe ist 46. Wie lautet die Zahl x? /5 P. 8. Löse die untenstehenden Aufgaben und schreibe das Ergebnis auf die dafür vorgesehenen Linien 27 8 2 15 3 100 20 4 (16 7) 45 (10 20 5) 13 (17 12) 24 4 55 12 6 27 3 8 (12 7) (13 7) 544 16 16 200 5 3 /3,5 P. 9. Setze eine Klammer so, dass das grösst mögliche Ergebnis entsteht. Schreibe die Lösung anschliessend auf die Linie. 89*5 54*3 13 2*34*4 10 8 6 4 /2 P. 10. Setze eine Klammer so, dass das Ergebnis stimmt. 8 20 12 64 143 88 29 84 400 80 16 24 44 16 4 2 3 18 /2 P. Maximale Punktzahl: 42 P. Erreichte Punktzahl: Note: Unterschrift der Eltern: Mathematikprüfung «Zahlenbegriffe und Klammern» (P) 1. Ergänze die Proportionalitätstabellen. Ein Zehnrappenstück wiegt 3,00 g. Anzahl Zehnrappenstück 5 Gewicht [g] 10 15 30 50 100 150 1000 Legt man 40 Fünfzigrappenstücke aufeinander, so wird der Turm 5 cm hoch. Anzahl Fünfzigrappenstüc 2 ke Höhe Turm [cm] 4 8 12 20 40 100 104 5 Für den Betrag von 0.50 Fr. braucht es 10 Fünfräppler. Betrag [Fr.] 0.20 0.40 0.50 0.80 Anzahl Fünfräppler 1 1.60 2 5 10 10.20 10 /6 P. 2. Welche Tabellen sind Proportionalitätstabellen? proportional 1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 nicht proportional proportional 1 2 3 4 40 5 50 6 60 70 7 80 8 9 nicht proportional proportional 20 30 90 100 0,4 0,8 1,2 1,6 2 2,4 2,8 3,2 2 4 6 8 10 12 14 16 nicht proportional 1,5 3 4,5 6 7,5 9 0,5 1 1,5 2 2,5 3 1 10,5 12 3,5 4 proportional nicht proportional proportional F 5 3 10 6 15 9 20 12 25 15 30 18 35 21 40 24 nicht proportional proportional 45 1 3 6 9 12 15 18 21 24 4 12 24 36 48 60 72 84 96 nicht proportional /6 P. 3. Ergänze die drei Tabellen. Welche sind Proportionalitätstabellen? 1 Liter Benzin kostet an der Tankstelle 1.50 Fr. Anzahl Liter 1 Preis [Fr.] 2 10 20 25 30 40 1.5 Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. Schneidet man eine Schnur in Stücke mit einer Länge von 10 cm, so gibt es 36 Stücke. Wie viele Stücke gibt es jeweils, wenn man die Länge eines Stückes wie folgt wählt? Länge eines Stückes 6 9 10 12 30 40 60 [cm] Anzahl Stücke 36 Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. Mirko sagt eine Zahl. Judith sagt darauf eine Zahl, die jeweils um 5 grösser ist. Mirko sagt: 1 3 5 10 15 50 95 100 Judith sagt: Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. /6,5 P. 4. Übermale alle Quadratzahlen in der untenstehenden Tabelle mit einem roten Farbstift. /5 P. 5. Schreibe die Primfaktorzerlegung folgender Zahlen auf. Schreibe deine Lösung anschliessend auch als Potenzschreibweise auf. Zahlen Primfaktorzerlegung Potenzschreibweis 156 135 265 410 123 190 210*105 189*119 /5 P. 6. Was ist spezielle an einer Primzahl. Erkläre in einem ganzen Satz. /1 P. 7. Schreibe die Rechnung der Zahlenrätsel auf die Linie unter dem entsprechenden Rätsel und die Lösung in das Kästchen am rechten Rand. Die Differenz aus einer Zahl und dem Subtrahenden 8 wird mit dem Produkt des Faktors 6 mit sich selbst addiert. Die daraus entstehende Summe ist 46. Wie lautet die Zahl x? Ich denke mir eine Zahl und dividiere sie mit dem Dividenden 12. Der Quotient dieser beiden Zahlen wird anschliessend mit dem Faktor 9 verrechnet und von dem entstandenen Ergebnis der Subtrahend 7 abgezogen. Die dadurch entstandene Differenz ist 20. An welche Zahl habe ich gedacht? Der Quotient von und dem Divisor 5 wird mit dem Summand 23,5 addiert und anschliessend vom Minuend 44,5 abgezogen. Die dadurch entstandene Differenz beträgt 16. Wie lautet die Zahl x? Vom 6 Fachen einer Zahl wird der Subtrahend 16,2 abgezogen und die Differenz anschliessend mit dem Faktor 15 multipliziert. Wird zu dem Ergebnis anschliessend die Zahl 75 addiert so erhält man 300. Wie lautet die Zahl x? Das Doppelte einer Zahl wird vom Minuenden 17 abgezogen und anschliessend mit dem Faktor 16,9 multipliziert. Teil man das daraus entstehende Produkt mit dem Divisor 13 und addiert zu dem Quotienten die Quadratzahl von 6 so erhält man die Quadratzahl von 7. Wie lautet die Zahl x? /5 P. 8. Löse die untenstehenden Aufgaben und schreibe das Ergebnis auf die dafür vorgesehenen Linien 8 (12 7) (13 7) 55 12 6 27 (45 5 6) 27 8 2 (4 (10 36 6) 1) 3 4 (8 9 ( 30 2 6) 16,5) 20 4 (16 7) (7 (6 3 5 4)) (10 20 5) 13 (17 (24,5 15 15 10)) 24 4 (9 (7 7 6 8 8)) *12 55 8 4 7 3 /3,5 P. 9. Setze eine Klammer so, dass das grösst mögliche Ergebnis entsteht. Schreibe die Lösung anschliessend auf die Linie. 89*5 5 4 3 13 2*34*4 10 8 6 4 /2 P. 10. Setze eine Klammer so, dass das Ergebnis stimmt. 400 80 16 9 49 4 16 6 4 55 - * 2 5 9 24 44 117 3 18 10 30 /2 P. Maximale Punktzahl: 42 P. Erreichte Punktzahl: Note: Unterschrift der Eltern: Mathematikprüfung «Zahlenbegriffe und Klammern» (A) 1. Ergänze die Proportionalitätstabellen. Ein Zehnrappenstück wiegt 3,00 g. Anzahl Zehnrappenstücke 5 10 15 30 50 100 150 1000 Gewicht [g] Legt man 40 Fünfzigrappenstücke aufeinander, so wird der Turm 5 cm hoch. Anzahl Fünfzigrappenstück 2 Höhe Turm [cm] 4 8 12 20 40 100 104 5 Für den Betrag von 0.50 Fr. braucht es 10 Fünfräppler. Betrag [Fr.] 0.20 0.40 0.50 0.80 Anzahl Fünfräppler 10 1 1.60 2 5 10 10.20 /6 P. 2. Welche Tabellen sind Proportionalitätstabellen? proportional 1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 nicht proportional proportional 1 2 3 4 40 5 50 6 60 70 7 8 80 9 nicht proportional proportional 20 30 90 100 0,4 0,8 1,2 1,6 2 2,4 2,8 3,2 2 4 6 8 10 12 14 16 nicht proportional 1,5 3 4,5 6 7,5 9 0,5 1 1,5 2 2,5 3 10,5 12 3,5 proportional nicht proportional 4 proportional y 1 5 3 10 6 15 9 20 12 25 15 30 18 21 35 40 24 nicht proportional proportional 45 x 1 3 6 9 12 15 18 21 24 4 12 24 36 48 60 72 84 96 nicht proportional /6 P. 3. Ergänze die drei Tabellen. Welche sind Proportionalitätstabellen? 1 Liter Benzin kostet an der Tankstelle 1.50 Fr. Anzahl Liter Preis [Fr.] 1 2 10 1.5 Das ist eine Proportionalitätstabelle. 20 25 30 40 Das ist keine Proportionalitätstabelle. Schneidet man eine Schnur in Stücke mit einer Länge von 10 cm, so gibt es 36 Stücke. Wie viele Stücke gibt es jeweils, wenn man die Länge eines Stückes wie folgt wählt? Länge eines Stückes 6 9 10 12 30 40 60 [cm] Anzahl Stücke 36 Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. Mirko sagt eine Zahl. Judith sagt darauf eine Zahl, die jeweils um 5 grösser ist. Mirko sagt: 1 3 5 10 15 50 95 100 Judith sagt: Das ist eine Proportionalitätstabelle. Das ist keine Proportionalitätstabelle. /6,5 P. 4. Übermale alle Quadratzahlen in der untenstehenden Tabelle mit einem roten Farbstift. /5 P. 5. Schreibe die Primfaktorzerlegung folgender Zahlen auf. Schreibe deine Lösung anschliessend auch als Potenzschreibweise auf. Zahlen Primfaktorzerlegung Potenzschreibweise 18 25 40 88 49 27 90 56 46 38 /5 P. 6. Was ist spezielle an einer Primzahl. Erkläre in einem ganzen Satz. /1 P. 7. Schreibe die Rechnung der Zahlenrätsel auf die Linie unter dem entsprechenden Rätsel und die Lösung in das Kästchen am rechten Rand. Ich denke mir eine Zahl, addiere 12 dividiere das Ergebnis durch 11 und multipliziere den Quotienten anschliessend mit 2. Das daraus entstehende Produkt ist 22. Welche Zahl habe ich mir gedacht? Addiert man zu einer Zahl den Summanden 16,5 und subtrahiert dann die Zahl 7,2, so erhält man die Differenz 40. Wie lautet die Zahl ? Ich denke mir eine Zahl, dividiere diese durch 12 und addiere anschliessend 18. Die Summe verdreifache ich und erhalte 90. Welche Zahl habe ich mir gedacht? Subtrahiert man 12 von dem Minuenden und multipliziert die Differenz anschliessend mit 14 so erhält man 196. Wie heisst die Zahl x? Ich denke mir eine Zahl und dividiere sie mit dem Dividenden 12. Der Quotient dieser beiden Zahlen wird anschliessend mit dem Faktor 9 verrechnet und von dem entstandenen Ergebnis der Subtrahend 7 abgezogen. Die dadurch entstandene Differenz ist 20. An welche Zahl habe ich gedacht? /5 P. 8. Löse die untenstehenden Aufgaben und schreibe das Ergebnis auf die dafür vorgesehenen Linien 4 30 2 8 600 (5 3 2) 300 600 6 3 800 200 5 3 27 8 2 15 3 100 20 4 (16 7) 45 (10 20 5) /3,5 P. 9. Setze eine Klammer so, dass das grösst mögliche Ergebnis entsteht. Schreibe die Lösung anschliessend auf die Linie. 89*5 54*3 13 2*34*4 10 8 6 4 /2 P. 10. Setze eine Klammer so, dass das Ergebnis stimmt. 400 80 16 24 398 8 143 5 20 88 7 12 64 29 9 84 108 /2 P. Maximale Punktzahl: 42 P. Erreichte Punktzahl: Note: Unterschrift der Eltern: