Arbeitsblatt: Proportionale Zuordnungen

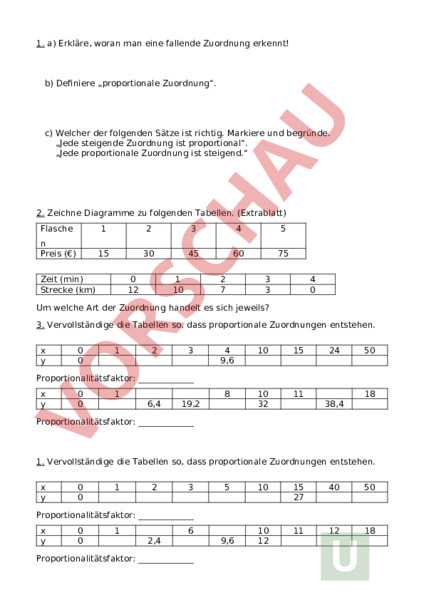
1. a) Erkläre, woran man eine fallende Zuordnung erkennt! b) Definiere „proportionale Zuordnung. c) Welcher der folgenden Sätze ist richtig. Markiere und begründe. „Jede steigende Zuordnung ist proportional. „Jede proportionale Zuordnung ist steigend. 2. Zeichne Diagramme zu folgenden Tabellen. (Extrablatt) Flasche 1 2 3 4 5 Preis (€) 15 30 45 60 75 Zeit (min) Strecke (km) 0 12 1 10 2 7 3 3 4 0 Um welche Art der Zuordnung handelt es sich jeweils? 3. Vervollständige die Tabellen so, dass proportionale Zuordnungen entstehen. y 0 0 1 2 3 4 9,6 10 15 8 10 32 11 24 50 Proportionalitätsfaktor: y 0 0 1 6,4 19,2 18 38,4 Proportionalitätsfaktor: 1. Vervollständige die Tabellen so, dass proportionale Zuordnungen entstehen. y 0 0 1 2 3 5 10 15 27 40 50 10 12 11 12 18 9,6 Proportionalitätsfaktor: y 0 0 1 6 2,4 Proportionalitätsfaktor: 2. a) Welcher der folgenden Sätze ist richtig. Markiere und begründe. „Jede steigende Zuordnung ist proportional. „Jede proportionale Zuordnung ist steigend. b) Erkläre, woran man eine fallende Zuordnung erkennt! c) Definiere „proportionale Zuordnung. 3. Zeichne Diagramme zu folgenden Tabellen. (Extrablatt) Zeit (min) Strecke (km) 0 2 1 4 2 5 3 7 4 8 Zeit (Stunden) Topflappen 1 5 2 10 3 15 4 20 5 25 Um welche Art der Zuordnung handelt es sich jeweils? Wiederholung zum Thema ZUORDNUNGEN 1. a) Erkläre mit mathematischen Begriffen, woran man eine fallende Zuordnung (auch ohne Diagramm) erkennt! b) Einer der folgenden Sätze ist richtig, einer ist falsch. Schreibe ab, markiere mit „richtig und begründe bzw. markiere mit „falsch und finde ein Gegenbeispiel. Jede steigende Zuordnung ist proportional. Jede proportionale Zuordnung ist steigend. 2. Zeichne Diagramme zu folgenden Tabellen. (Extrablatt) Achte beim Zeichnen auf folgende Regeln: mit spitzem Bleistift und Lineal zeichnen auf kariertem Papier möglichst genau zeichnen die Größe, die in der Tabelle oben steht, ist die „unabhängige Größe (man kann sich aussuchen, wie viele Flaschen Wein man kaufen möchte), sie wird an der Rechtsachse aufgetragen. Die Größe, die unten steht, ist die „abhängige Größe (der Preis, den ich für den Wein zahlen muss, hängt davon ab, wie viele Flaschen Wein ich kaufe), sie wird an der Hochachse aufgetragen. wenn es um eine abstrakte Zuordnung geht, bezeichnet man die Rechtsachse mit „x und die Hochachse mit „y. Wenn es hingegen um etwas Konkretes geht, trägt man an die Enden der Achse genau dies ein (z.B. Länge (cm), Preis (€), Zeit (min).) man schreibt in sinnvoller Weise Zahlen an die Achsen. Auf jeden Fall beginnen beide Achsen mit Null und die Abstände zwischen den Zahlen sind gleichgroß die Achsen „enden mit einer Pfeilspitze (sauber und schlank) man überlegt, ob es sinnvoll ist, die Punkte zu verbinden (gibt es die Zwischenwerte bei dieser Zuordnung überhaupt?) a) Flaschen Preis (€) b) Zeit (min) Strecke (km) c) Zeit (min) Strecke (km) d) Hühner Eier pro Woche 1 15 2 30 3 45 4 50 5 65 0 12 1 10 2 7 3 3 4 0 0 0 1 1,5 2 3 3 4,5 4 6 1 4 2 8 3 12 4 16 5 20 3. Vervollständige die Tabellen so, dass proportionale Zuordnungen entstehen. Denke daran: Wird bei einer proportionalen Zuordnung die eine Größe verdoppelt (verdreifacht, vervierfacht . ), wird auch die andere Größe verdoppelt (verdreifacht, vervierfacht.). Natürlich gilt auch: Halbierung der einen Größe, führt zur Halbierung der anderen Größe usw. Man kann sich dies mit Pfeilen deutlich machen. y a) y 0 0 0 0 1 1 2 4 10 560 280 2 3 4 9,6 10 15 8 10 32 11 24 50 Proportionalitätsfaktor: b) y 0 0 1 6,4 19,2 Proportionalitätsfaktor: c) 18 38,4 0 1 2 3 0 Proportionalitätsfaktor: d) y 0 0 1 5 10 15 27 40 50 11 12 18 9,6 10 12 6 2,4 Proportionalitätsfaktor: