Arbeitsblatt: KA_9JG_Zuordnungen-Funktionen

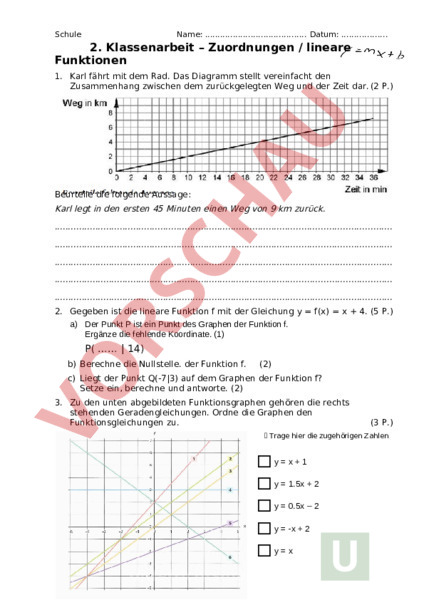
Schule Name: Datum: 2. Klassenarbeit – Zuordnungen lineare Funktionen 1. Karl fährt mit dem Rad. Das Diagramm stellt vereinfacht den Zusammenhang zwischen dem zurückgelegten Weg und der Zeit dar. (2 P.) Beurteile die folgende Aussage: Karl legt in den ersten 45 Minuten einen Weg von 9 km zurück. 2. Gegeben ist die lineare Funktion mit der Gleichung f(x) x 4. (5 P.) a) Der Punkt ist ein Punkt des Graphen der Funktion f. Ergänze die fehlende Koordinate. (1) P( 14) b) Berechne die Nullstelle. der Funktion f. (2) c) Liegt der Punkt Q(-73) auf dem Graphen der Funktion f? Setze ein, berechne und antworte. (2) 3. Zu den unten abgebildeten Funktionsgraphen gehören die rechts stehenden Geradengleichungen. Ordne die Graphen den Funktionsgleichungen zu. (3 P.) Trage hier die zugehörigen Zahlen ein! yx1 1.5x 2 0.5x – 2 -x 2 yx Schule Name: Datum: y3 2. Klassenarbeit – Zuordnungen lineare Funktionen 4. Ein Flugzeug besitzt einen Treibstoffvorrat von 10.500 Liter Kerosin. Auf 100km verbraucht es 180 Liter. (5 P.) a) Erstelle eine Wertetabelle, die dir für die geflogenen Kilometer den Verbrauch in Liter anzeigt. Wähle dafür eine Strecke von 0 km bis 5.000 km; über die Aufteilung der Wertepaare entscheidest du selbst. (3) b) Nach wie vielen Kilometern (km) wäre der Treibstoffvorrat aufgebraucht? Berechne! (2) -------------------------------------------------------------- Wahlaufgabe (5.) – Wähle zwischen , oder 5. Das Schaubild zeigt, wie das Wasser aus zwei gleichen Regentonnen ausläuft. Beschreibe (unter Verwendung der Fachbegriffe) die Auslaufvorgänge beider Tonnen. (4 P.) Zusatz: Wie lauten die Funktionsgleichungen? Gib sie an! ------------------------------------------------------- (2 P.) Schule Name: Datum: 2. Klassenarbeit – Zuordnungen lineare Funktionen Wahlaufgabe (5.) – Wähle zwischen , oder 5. Die Wertetabelle gehört zu einer linearen Funktion f. (8 P.) a) Stelle die zugehörige Funktionsgleichung auf. (1) b) Zeichne den Graph der Funktion f. (2) c) Eine weitere Gerade einer Funktion schneidet die y-Achse bei 3 und geht durch den Punkt (2 2). Bestimme die Funktionsgleichung. (2) d) Zeichne den Graph der Funktion in das gleiche Koordinatensystem. (2) e) Gib die Nullstelle für die Funktion an! (1) Zusatz: Bestimme den Schnittpunkt der Funktionen und f. Gib ihn an! (2 P.) Schule Name: Datum: 2. Klassenarbeit – Zuordnungen lineare Funktionen Wahlaufgabe (5.) – Wähle zwischen , oder 5. Ein Fallschirmspringer öffnet seinen Fallschirm und misst mit Hilfe eines Höhenmeters zu verschiedenen Zeitpunkten nach dem Öffnen des Schirmes seine Höhe über dem Erdboden. (11 P.) Die Messung ergab die folgende Wertetabelle: a) Begründe, dass der Zusammenhang zwischen (Fall)Zeit und Höhe durch eine lineare Funktion beschrieben werden kann. (2) b) Stelle den Funktionsgraphen im Koordinatensystem dar und gib die Funktions-gleichung an. (5) c) Nach welcher (Fall)Zeit erreicht der Fallschirmspringer den Boden? (2) d) Nach seiner Landung gibt der Fallschirmspringer an, dass er sich nach einer Fallzeit von 2 Minuten in einer Höhe von weniger als 100 befand. Kann das sein? Überprüfe die Aussage rechnerisch und nimm Stellung dazu! (2) Schule Name: Datum: Schule Name: Datum: 2. Klassenarbeit – Zuordnungen lineare Funktionen Wahlaufgabe (6.) – Wähle zwischen , oder 6. Kanuwanderung (6 P.) Bei einer Kanuwanderung auf der Dahme starten die teilnehmenden Boote stündlich von der Anlegestelle. Das rote Boot fährt mit einer Geschwindigkeit von 1,5 km/h. Im Diagramm ist die Abhängigkeit der gefahrenen Strecke von der Zeit dargestellt. a) Welche Strecke hat das rote Boot um 10:00 Uhr zurückgelegt? Gib die Entfernung an! (1) b) Um wie viel Uhr ist das rote Boot 4,5 km von der Anlegestelle entfernt? Gib die Uhrzeit an! (1) Das blaue Boot fährt zwei Stunden später von der gleichen Anlegestelle mit einer durchschnittlichen Geschwindigkeit von 3 km/h ab. c) Stelle für das blaue Boot diese Abhängigkeit in demselben Diagramm dar! (2) d) Zu welcher Uhrzeit überholt das blaue Boot das rote? Gib die Uhrzeit an! (2) Lies entweder den Punkt aus den Graphen ab oder berechne den speziellen Punkt. -------------------------------------------------------------- Schule Name: Datum: Schule Name: Datum: 2. Klassenarbeit – Zuordnungen lineare Funktionen Wahlaufgabe (6.) – Wähle zwischen , oder 6. Die Schnecken Schnick und Schnack a) (8 P.) Schnick kriecht mit konstanter Geschwindigkeit von 4 cm/min von einem Baum weg. (3) Lege dazu eine Wertetabelle für die ersten vier Minuten an! Beginne bei 0 min! Stelle den Zusammenhang zwischen Weg und Zeit für die ersten vier Minuten in einem Diagramm dar! (Zeichne den zugehörigen Graphen!) Stelle diesen Sachverhalt in einer Funktionsgleichung dar. Schnick Schnack zurückgelegter Weg (s) in Zeit (t) in min cm Funktionsgleichung Schnick: Funktionsgleichung Schnack: b) Schnack hat bereits einen Weg von 4 cm zurückgelegt und bewegt sich mit der gleichen Geschwindigkeit wie Schnick. (3) a) Stelle auch hierzu eine Wertetabelle für die ersten vier Minuten auf! Beginne bei 0 min! b) Stelle den Zusammenhang zwischen Weg und Zeit auch für Schnack grafisch im Schule Name: Datum: selben Diagramm wie von Schnick dar. Schule Name: Datum: 2. Klassenarbeit – Zuordnungen lineare Funktionen Wahlaufgabe (6.) 6. Die Schnecken Schnick und Schnack Fortsetzung c) Kreuze die zutreffende Aussage zum Fortbewegungsverlauf von Schnick Schnack an und begründe unten! (2) Der Abstand zwischen Schnick und Schnack wird im Verlauf der Zeit immer größer, weil Schnick holt irgendwann Schack ein, weil Beide Schnecken haben immer den gleichen Abstand zueinander, weil Deine Begründung: -------------------------------------------------------------- Wahlaufgabe (6.) – Wähle zwischen , oder 6. Urlaub mit dem Wohnmobil (13 P.) Familie Meier plant eine siebentägige Urlaubsfahrt mit einem Wohnmobil. Dazu holt sie sich drei Angebote von Verleihfirmen ein. Die Angebote lauten: Firma A: 25 € pro Tag zuzüglich 0,20 € pro gefahrene Kilometer Firma B: 30 € pro Tag zuzüglich 0,15 € pro gefahrene Kilometer Firma C: 45 € pro Tag zuzüglich 0,10 € pro gefahrene Kilometer a) Von welcher Firma sollte sich Familie Meier das Wohnmobil ausleihen, wenn die Reise ca. 1500 km lang ist? Berechne und beantworte! (3) b) Für welche Streckenlängen sind die beiden anderen Firmen günstiger? (2) c) Stelle den Zusammenhang von gefahrenen Kilometern und Gesamtkosten tabellarisch für eine Streckenlänge von 0 km bis 1000 km in Schritten von 100 km für die Firmen und dar. (5) Beachte die siebentägige Urlaubsfahrt. d) Stelle den Sachverhalt aus c) in ein und demselben Koordinatensystem dar. Was lässt sich aus der grafischen Darstellung ablesen? (3) Schule Name: Datum: Eine Vorlage eines Koordinatensystems findest du auf der nächsten Seite! 2. Klassenarbeit – Zuordnungen lineare Funktionen Wahlaufgabe (6.) 6. Urlaub mit dem Wohnmobil Fortsetzung Koordinatensystem zu 6. d) max. erreichbar: Schule Name: Datum: G-Niveau (25 P.) E-Niveau (39 P.)