Arbeitsblatt: Zusatzuübungen Mathbuch 3+

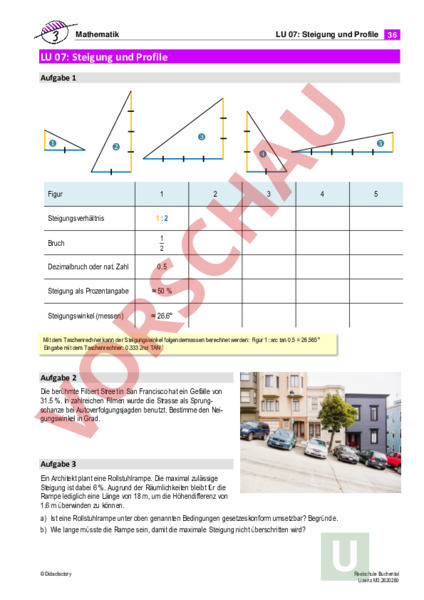
Mathematik LU 07: Steigung und Profile 36 LU 07: Steigung und Profile Aufgabe 1 Figur Steigungsverhältnis Bruch 1 2 3 4 5 1:2 1 2 Dezimalbruch oder nat. Zahl 0.5 Steigung als Prozentangabe 50 Steigungswinkel (messen) 26.6 Mit dem Taschenrechner kann der Steigungswinkel folgendermassen berechnet werden: Figur 1: arc tan 0.5 26.565 Eingabe mit dem Taschenrechner: 0.333 2nd TAN-1 Aufgabe 2 Die berühmte Filbert Street in San Francisco hat ein Gefälle von 31.5 %. In zahlreichen Filmen wurde die Strasse als Sprungschanze bei Autoverfolgungsjagden benutzt. Bestimme den Neigungswinkel in Grad. Aufgabe 3 Ein Architekt plant eine Rollstuhlrampe. Die maximal zulässige Steigung ist dabei 6 %. Augrund der Räumlichkeiten bleibt für die Rampe lediglich eine Länge von 18 m, um die Höhendifferenz von 1.6 überwinden zu können. a) Ist eine Rollstuhlrampe unter oben genannten Bedingungen gesetzeskonform umsetzbar? Begründe. b) Wie lange müsste die Rampe sein, damit die maximale Steigung nicht überschritten wird? Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 07: Steigung und Profile 37 Aufgabe 4 Auf der Südseite eines Hausdaches werden Solarzellen montiert. Höhe (m) a) Bestimme die fehlenden Werte in der Tabelle. Steigungsverhältnis 8 7 Bruch 6 Dezimalbruch 5 Steigung als Prozentangabe 4 3 Steigungswinkel b) Um möglichst viel Energie zu gewinnen, sollte das Dach mit Südausrichtung eine Neigung von ungefähr 60 haben (ca. 31). Wie gross müsste die Höhe des Dachstuhles sein? 2 1 0 1 2 3 4 5 6 7 8 9 Breite (m) Aufgabe 5 Eine der bekanntesten Etappen der Tour de France ist jene auf die Alpe dHuez. Die steile Passstrasse wird jeweils von Tausenden von Fans gesäumt. Auf der Homepage der Tour de France findet man ein Streckenprofil der spektakulären Etappe. Streckenprofile werden meist überhöht dargestellt. a) Berechne die durchschnittliche Steilheit in Prozent der ersten Abfahrt von Modane nach Saint-Jean-de-Maurienne. b) Berechne die durchschnittliche Steilheit des berühmten Streckenabschnitts zwischen Bourg-dOisans und Huez Village. c) Zeichne ein nicht überhöhtes Profil des berühmten Streckenabschnittes Bourg-dOisans – Huez Village. Verwende den Massstab 1:100‘000 (1 km 1 cm). Streckenprofil: Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 07: Steigung und Profile 38 Aufgabe 6 Kleingaragen sollten bei der Einfahrt nicht steiler als 20 sein. Ausserdem müssen die Neigungsübergänge abgeflacht sein, damit das Auto nicht aufsitzt. a) Bestimme die Steigung einer Einfahrt, welche auf 5 genau 92.5 cm ansteigt. b) Herr Sturzenegger plant für die Einfahrt seiner neuen Garage auf 18 Länge eine Höhe von 4 zu überwinden. Er fragt dich um Rat, ob das eine vernünftige Neigung ist. Beurteile. Aufgabe 7 6m 49 25 18 Schaufigur 5m 56 1 40 2m 2 15 3 12 4 5 Steigungsverhältnis gekürzt Dezimalbruch oder nat. Zahl Steigung als Prozentangabe Steigungswinkel* Miker, Shutterstock.com Aufgabe 8 Von einer Skateboardrampe ist bekannt, dass 2.44 und 2.40 beträgt. Wie steil ist die Rampe in %? b Aufgabe 9 Beim Bau einer Eisenbahn durch eine Ebene muss eine Rampe errichtet werden, damit die Gleise einen Fluss auf einer Höhe von 18 über der Ebene überqueren können. Die Bahn muss so hoch geführt werden, da der Fluss für die Schiffahrt genutzt wird. Züge können eine Steilheit von maximal 30 ‰ überwinden. Wie lange muss die Rampe mindestens werden? Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 07: Steigung und Profile 39 Aufgabe 10 Das italienische Dörfchen Viganella (1‘012 ü. M.) liegt in einem so engen Bergtal, dass die Sonne im Winter während 83 Tagen nicht auf das Dorf scheint. Deshalb liess die Gemeinde einen Spiegel am Berghang montieren, der 500 höher als der Dorfplatz liegt. Der 40 m2 grosse, vertikale Spiegel bringt immerhin einige Quadratmeter Sonnenlicht auf den Dorfplatz. Das Licht fällt mit einem Winkel von ca. 33.7 auf das Dorf. Wie weit ist der Spiegel vom Dorfplatz entfernt? Konstruiere das entsprechende Steigungsdreieck in einem geeigneten Massstab und lies das Ergebnis aus deiner Konstruktion heraus. Aufgabe 11 Stanserhorn (1‘868 m) Blattli (1564 m) Chälti (713 m) Cholplätzli (810 m) Wässerli (1050 m) Rinderalp (1635 m) Chalcherli (1165 m) Dorfplatz (452 m) swisstopo, BFL 0 km 2.1 km 2.7 km 4.4 km 5.3 km 8.3 km 9.7 km Das Bild zeigt das Streckenprofil des Berglaufes auf das Stanserhorn. a) Bestimme die durchschnittliche Steigung zwischen Chalcherli und Blatti in Prozent. b) Welcher der drei Streckenabschnitte Chälti-Cholplätzli, Cholplätzli-Wässerli oder Wässerli-Chalcherli ist am steilsten? c) Toni Jöhl aus Amden lief die Strecke im Jahr 2005 in einer Rekordzeit. Damals benötigte er im Schnitt für hundert Höhenmeter rund 4 min 23.08 s. In welcher Zeit bewältigte er den ganzen Berglauf? Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 07: Steigung und Profile 40 Aufgabe 12 Die Silverstar im Europapark gehört zu den spektakulärsten und höchsten Achterbahnen in Europa. An der steilsten Stelle fährt der Zug ein Gefälle von 68.5 hinunter. Zeichne eine Schaufigur, welche diese Steilheit darstellt und miss die Steigung in Grad. Aufgabe 13 Kurz nach einem Bahnhof führt das Gleis einer Zuglinie über eine Strasse. Allerdings ist die Überführung für Lastwagen unpassierbar, weshalb die Bahntrasse höher gelegt werden soll, so dass 4 hohe LKW passieren können. Die Gleise würden dafür vom Bahnhof aus 4.8 an Höhe gewinnen müssen. Bis anhin war die Unterführung lediglich 3.5 hoch und die Eisenbahntrasse 21 ‰ steil. Die Rampenlänge vom Bahnhof bis zur Strasse kann nicht verlängert werden. a) Die maximal zulässige Steigung beträgt 30 ‰. Kann das Projekt wie geplant durchgeführt werden? Begründe. b) Wie viel Höhe könnte vom Bahnhof aus bis zur Rampe maximal überwunden werden? c) Was wäre eine Alternative, falls die Steigung zu gross würde? Aufgabe 14 Die Schrägseilbrücke «Pont de Normandie», die Le Havre mit Honfleur verbindet, gilt mit ihren 2141 Spannweite als die grösste in Europa. Die 1995 eröffnete Strassenbrücke erreicht eine maximale Höhe von 215 m. Die Fahrzeuge überqueren die Seine auf einer Höhe von 59 und überwinden in der Anfahrt eine Steigung von 6 %. a) Wie vielen Grad entspricht die Steigung 6 %? b) Zeichne ein Steigungsdreieck der maximalen Neigung. Aufgabe 15 Wie gross ist jeweils die Steigung in Prozent, wenn von einem Steigungsdreieck folgende Angaben bekannt sind. a) Die horizontale Strecke ist 25 kleiner als die Schrägstrecke. b) Die Schrägstrecke ist doppelt so lang wie der Höhenunterschied. c) Der Höhenunterschied ist dreimal kleiner als die Schrägstrecke. d) Die Schrägstrecke ist 140 der Länge der horizontalen Strecke. e) Die horizontale Strecke ist 1.6 Mal so lang wie der Höhenunterschied. Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 12 und LU 15: Funktionen und Graphen 41 LU 12 und LU 15: Funktionen und Graphen Aufgabe 1 Bestimme die Funktion des blau gefärbten Graphen Schritt für Schritt und notiere sie in folgender Form. Funktionsgleichung: ax b 6 5 4 1. Steigung a: 3 2. Verschiebung b: 2 1 3. Funktionsgleichung: 0 1 2 3 4 6 5 7 8 9 Aufgabe 2 Bestimme die fehlenden Werte der folgenden Funktionen. a) b) 1 1 1 1. Steigung a: 1. Steigung a: 2. Verschiebung b: 2. Verschiebung b: Funktionsgleichung: Funktionsgleichung: c) 1 d) 1 1 1 1. Steigung a: 1. Steigung a: 2. Verschiebung b: 2. Verschiebung b: Funktionsgleichung: Funktionsgleichung: Didacfactory 1 Realschule Buchental Lizenz M3.2620260 Mathematik LU 12 und LU 15: Funktionen und Graphen 42 Aufgabe 3 Beispiel Gegeben sind die Punkte A(3/2) und B(7/4), trage sie ins Koordinatensystem ein und verbinde sie mit einer Geraden. Löse analog Gegeben sind die Punkte A(0/2) und B(7/1), trage sie ins Koordinatensystem ein und verbinde sie mit einer Geraden. (3/2) (7/4) 1 1 1 Bestimme die Steigung a. 4–2 7–3 2 1 4 2 Setze die Steigung in die Funktionsgleichung ein. 1 Bestimme die Steigung a. Setze die Steigung in die Funktionsgleichung ein. 1 y xb 2 Setze einen der beiden Punkte in die Funktionsgleichung ein. Setze einen der beiden Punkte in die Funktionsgleichung ein. 1 2 3b 2 Löse die Gleichung nach auf. b Löse die Gleichung nach auf. 1 2 Notiere die vollständige Funktionsgleichung. 1 1 2 2 y x Teste die Funktionsgleichung mit dem zweiten Punkt. 1 1 2 2 4 7 Didacfactory Notiere die vollständige Funktionsgleichung. Teste die Funktionsgleichung mit dem zweiten Punkt. Realschule Buchental Lizenz M3.2620260 Mathematik LU 12 und LU 15: Funktionen und Graphen 43 Aufgabe 4 Gegeben sind die Punkte A(2/–1) und B(5/3), trage sie ins Koordinatensystem ein und verbinde sie mit einer Geraden. Gegeben sind die Punkte A(2/1) und B(5/–1), trage sie ins Koordinatensystem ein und verbinde sie mit einer Geraden. 1 1 1 1 Bestimme die Steigung a. Bestimme die Steigung a. Setze die Steigung in die Funktionsgleichung ein. Setze die Steigung in die Funktionsgleichung ein. Setze einen der beiden Punkte in die Funktionsgleichung ein. Setze einen der beiden Punkte in die Funktionsgleichung ein. Löse die Gleichung nach auf. Löse die Gleichung nach auf. Notiere die vollständige Funktionsgleichung. Notiere die vollständige Funktionsgleichung. Teste die Funktionsgleichung mit dem zweiten Punkt. Teste die Funktionsgleichung mit dem zweiten Punkt. Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 12 und LU 15: Funktionen und Graphen 44 Aufgabe 5 Gegeben sind die Punkte A(1/–2) und B(2/2), trage sie ins Koordinatensystem ein und verbinde sie mit einer Geraden. Gegeben sind die Punkte A(1/4) und B(6/–3), trage sie ins Koordinatensystem ein und verbinde sie mit einer Geraden. 1 1 1 1 Bestimme die Steigung a. Bestimme die Steigung a. Setze die Steigung in die Funktionsgleichung ein. Setze die Steigung in die Funktionsgleichung ein. Setze einen der beiden Punkte in die Funktionsgleichung ein. Setze einen der beiden Punkte in die Funktionsgleichung ein. Löse die Gleichung nach auf. Löse die Gleichung nach auf. Notiere die vollständige Funktionsgleichung. Notiere die vollständige Funktionsgleichung. Teste die Funktionsgleichung mit dem zweiten Punkt. Teste die Funktionsgleichung mit dem zweiten Punkt. Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 12 und LU 15: Funktionen und Graphen 45 Aufgabe 6 a) Auf der Geraden 6x – 2 liegt der Punkt P(x/4). b) Auf der Geraden Bestimme dessen x-Koordinate. 4 11 2 liegt der Punkt P(x/8). Bestimme dessen x-Koordinate. Aufgabe 7 a) Auf der Geraden –3x 0.6 liegt der Punkt P(5/y). b) Auf der Geraden Bestimme die y-Koordinate des Punktes. 7 2 4 – liegt der Punkt P(–3/y). 5 Bestimme die y-Koordinate des Punktes. Aufgabe 8 Der Punkt P(4/7) liegt auf der Geraden 1.5x b. a) Bestimme die Verschiebung b. b) Zeichne die Gerade in das nebenstehende Koordinatensystem ein. 1 1 Aufgabe 9 4 Von einer Funktionsgleichung kennt man und den Punkt P(6/2). a) Bestimme die Verschiebung b. b) Zeichne den Graphen und trage ein. 9 4 1 1 Didacfactory 9 Realschule Buchental Lizenz M3.2620260 Mathematik LU 12 und LU 15: Funktionen und Graphen 46 Aufgabe 10 2 Von einer Funktionsgleichung kennt man – und den Punkt P(–3/5). 3 a) Bestimme die Verschiebung b. b) Zeichne den Graphen und trage ein. 1 1 Aufgabe 11 Du findest auf der Strasse eine Zehnernote und gibst die folgenden zehn Tage je einen Franken für Süssigkeiten aus. 10 (CHF) a) Zeichne einen passenden Graphen zum Text. b) Bestimme grafisch die Koordinaten des Punktes am sechsten Tag. c) Wie heisst die Funktionsgleichung des Graphen? 1 (Tage) 1 10 Aufgabe 12 Eliane bekommt acht Franken und kauft damit jeden Tag für 1.50 CHF ein Gipfeli. a) Zeichne den Graphen. b) Bestimme graphisch, wie viel Geld Eliane nach 4 Tagen noch bleibt. c) An welchem Tag reicht das Geld nicht mehr? d) Wie heisst die Funktionsgleichung des Graphen? (CHF) 8 1 (Tage) 1 Didacfactory 10 Realschule Buchental Lizenz M3.2620260 Mathematik LU 12 und LU 15: Funktionen und Graphen 47 Aufgabe 13 Deine Eltern geben dir im Urlaub ein grosszügiges Taschengeld. Dies ist auch nötig, denn du gibst für die verschiedenen Sport- und Freizeitangebote vor Ort 50 CHF pro Tag aus. Das Geld reicht genau für sieben Tage. Wie sieht eine passende Funktionsgleichung dazu aus? Aufgabe 14 Kerstin macht in den Bergen Ferien. Das mitgenommenen Bargeld reicht für drei Tage. Am vierten Tag hat sie noch 35.70 €. in ihrer Brieftasche. Pro Tag benötigt Kerstin im Schnitt 102.65 €. a) Wie lautet die passende Funktionsgleichung? b) Bestimme den Punkt (Koordinaten) am Ende des zweiten Tages. Aufgabe 15 Mirjam kaufte sich kurz nach der Lehre ein Auto für 21200 CHF. Davon konnte sie 9700 CHF direkt aus ihren Ersparnissen bezahlen, den restlichen Betrag liehen ihr die Eltern. Es wurde vereinbart, dass Mirjam ihren Eltern monatlich 350 CHF zurückzahlt, bis die Schulden beglichen sind. a) Wie lange dauert es, bis Mirjam die Schulden beglichen hat? b) Wie lautet die passende Funktionsgleichung? Aufgabe 16 Du hast mit einem Nebenjob 45 Franken verdient. Davon kaufst du dir in der Bäckerei jeden Tag ein kleines Sandwich für vier Franken. a) Wie könnte eine passende Funktionsgleichung lauten? Wofür würden und stehen? b) Wie lange reicht das verdiente Geld? Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 48 LU 19: Lineare Funktionen und Gleichungssysteme Aufgabe 1 Löse die folgenden Gleichungssysteme a) mit dem Substitutionsverfahren. 1) 5y 2x – 5 2) –x6 4x 4y 24 3) 2y 5x 2y 66 4x b) mit dem Gleichsetzungsverfahren. 1) 12 – 2x 3y 2) 9y – 3x 9 10x – 2y 56 3) 3x – 2y y 2x 13 4y – 8 6y – 3 2x c) Entscheide selber, mit welchem Verfahren du die folgenden drei Aufgaben lösen möchtest. 1) –2x 6y 14 2) –4y – 3x 8 –x 2y –20 3) 8 4y x:35y–4 3y – 15 2x Aufgabe 2 Löse mit dem Substitutionsverfahren. Aufgabe 3 Löse mit dem Gleichsetzungsverfahren. Aufgabe 4 Löse die folgenden Gleichungssysteme. a) 4x 3 5y 3y 9 Didacfactory b) 5x 2y 14 xy c) 15x y 34 2x Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 49 Aufgabe 5 Löse die folgenden Gleichungssysteme. a) 2y 3x – 4 2 b) 2 3y 8y 2(x – y) 2y 15 c) 4x – 2y 6 3x –2y – 8 2y – 16 3x Aufgabe 6 Löse die folgenden Gleichungssysteme. a) 13 6x y 90 b) 4y 12x 20 2x – 2y 26 c) 15x – 36 3 6x 4y Aufgabe 7 Löse die folgenden Gleichungssysteme. a) 3 4 3 2 b) 4y 18 – 10 x– 9 6 y– x–2 7 c) 2 y–2x2 10 3.5 2 3x – 3y 3 Aufgabe 8 Löse die folgenden Gleichungssysteme. a) 8 5 b) 10 2 1 3 6 4 4 5 – 15 15 6 c) 3 y3– x3 7 – 2y 7 – 2 2 14 – 7 Aufgabe 9 Löse die folgenden Gleichungssysteme. a) 3 15 3 2 2 2x – – 4y– Didacfactory b) 2 3 5 2 x 6 3 c) 3y – 1 18x – 7 4 2 –3 1 10 3 3 x Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 50 Aufgabe 10 Von zwei Geraden sind jeweils ihre Funktionsgleichungen gegeben. Bestimme algebraisch ihre Schnittpunkte. a) 4x – 7 c) – 0.5x 15.5 b) – 15x 3 yx1 18x 20 d) 4x – 8 0.7x – 1.5 0.9x 3 Aufgabe 11 Trage die Geraden und in das Koordinatensystem ein. Die Funktionsgleichungen lauten für g: – 3x 8 und für h: 0.5x 1 Bestimme zuerst grafisch, dann algebraisch den Schnittpunkt der beiden Geraden. Grafische Lösung Algebraische Lösung 1 1 Aufgabe 12 Gegeben sind die Punkte A(–3/3), B(7/7), C(–2/–3) und D(0/1). Die Gerade führt durch die Punkte und B, die Gerade durch die Punkte und D. Bestimme die Funktionsgleichungen und den Schnittpunkt von und zuerst algebraisch, dann grafisch. Algebraische Lösung Grafische Lösung 1 1 Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 51 Aufgabe 13 Gegeben sind die Punkte A(–4/4), B(8/1), C(–8/–7) und D(0/7). Die Gerade führt durch die Punkte und B, die Gerade durch die Punkte und D. Bestimme die Funktionsgleichungen und den Schnittpunkt von und h. a) algebraisch b) grafisch Aufgabe 14 Gegeben sind die Punkte A(–3/5), B(12/0), C(3/–2) und D(9/6). Die Gerade führt durch die Punkte und B, die Gerade durch die Punkte und D. Bestimme die Funktionsgleichungen und den Schnittpunkt von und algebraisch. Aufgabe 15 Gegeben sind zwei Geraden mit den Funktionsgleichungen – 2 und 1. Bestimme den Schnittpunkt der beiden Geraden grafisch und algebraisch. grafische Lösung: algebraische Lösung: 1 1 x–2 Aufgabe 16 1 5 9 9 Gegeben sind zwei Geraden mit den Funktionsgleichungen 4 und 2 Bestimme den Schnittpunkt der beiden Geraden grafisch und algebraisch. grafische Lösung: algebraische Lösung: 1 1 Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 52 Aufgabe 17 5 Gegeben sind zwei Geraden mit den Funktionsgleichungen 3 und – 2 – 2. Bestimme den Schnittpunkt der Geraden algebraisch und grafisch. grafische Lösung: algebraische Lösung: 1 1 Aufgabe 18 Bestimme zuerst algebraisch und dann grafisch die Schnittpunkte der Geraden und h. a) g1 mit den Punkten A(–2/7) und B(6/1) h1 mit der Funktionsgleichung 2.5x – 1 b) g2 mit den Punkten C(0/3) und D(4/–2) h2 mit der Funktionsgleichung 0.25x – 3 1 1 Aufgabe 19 Bestimme algebraisch die Schnittpunkte der Geraden und h. a) g: 2x – 15 h: –3x 4 d) g: 1/3x – 1/3 : 3x 3 b) g: 0.5x 2.5 h: 0.25x 15 e) g: 20x – 25 h: 24x 2 c) g: 0.75x – 1 h: f) g: –1.5x 4.5 h: –4x 12 Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 53 Aufgabe 20 Liam und Moritz sind zurzeit zusammmen neun Jahre alt. In drei Jahren wird Liam doppelt so alt sein wie Moritz. Wie alt sind die beiden heute? Löse die Aufgabe nach der vorgegebenen Struktur. a) Fülle die Tabelle aus. Alter heute Moritz Alter in 3 Jahren Liam b) Notiere aus dem Zusammenhang zwei verschiedene Gleichungen. Gleichung 1 Gleichung 2 c) Forme die Gleichungen nach um (bilde Funktionsgleichungen). Gleichung 1 Gleichung 2 d) Zeichne die Graphen und lies den Schnittpunkt heraus. 10 e) Welche Bedeutung haben die KoordinatenSchnittpunkte? f) Bestimme den Schnittpunkt algebraisch. 1 1 10 Kontrolle: Aufgabe 21 Jochen und sein Nachbar Marvin sind heute zusammen 87 Jahre alt. Vor 12 Jahren war Jochen zweimal so alt wie Marvin. Wie alt sind beide heute? Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 54 Aufgabe 22 In den beiden Klassen einer 3. Oberstufe sind zusammen 41 Schüler und Schülerinnen. Da die Klassen sehr ungleich gross sind, müssen 3 Schüler aus der Klasse 3a in die Klasse 3b wechseln. Nach dem Wechsel ist in der Klasse 3a ein Schüler mehr als in der Klasse 3b. Wie gross waren die Klassen ursprünglich? a) Fülle die Tabelle aus. Bisher 3a Neu 3b b) Notiere aus dem Zusammenhang zwei verschiedene Gleichungen. Gleichung 1 Gleichung 2 c) Forme die Gleichungen nach um (bilde Funktionsgleichungen). Gleichung 1 Gleichung 2 d) Zeichne die Graphen und lies den ungefähren Schnittpunkt heraus. 40 e) Welche Bedeutung hat der KoordinatenSchnittpunkt? f) Bestimme den Schnittpunkt algebraisch. 5 5 50 Kontrolle: Aufgabe 23 Herr Kahn lässt seine Klasse abstimmen, ob sie auf der Schulreise lieber an einen See oder in die Berge möchten. Bei der ersten Abstimmung stimmen allerdings genau die eine Hälfte der Klasse für die Berge und die andere Hälfte für den See. Deshalb wiederholt Herr Kahn die Abstimmung am Ende der Lektion. Diesmal ist das Ergebnis eindeutig. Vier Fünftel der Klasse möchten nun an den See, nachdem sich 6 Schüler umentschieden haben. Wie viele Schüler sind in der Klasse? Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 55 Aufgabe 24 Nicolas und Oliver fliegen am 28. April nach New York. Beim Umsteigen im Flughafen Brüssel passiert das Missgeschick. Ein Dieb klaut Nicolas das Portemonnaie und erleichtert ihn dadurch um 300 $. Nicolas kann somit in New York nur noch 75 täglich ausgeben. Oliver kann sich einiges mehr leisten. Seine Ausgaben pro Tag belaufen sich auf 150 $. a) Zeichne die Graphen für die Ausgaben von Nicolas und Oliver (inklusive Diebstahl). b) Notiere die jeweiligen Funktionsgleichungen. c) Wann sind ihre Ausgaben gleich hoch? Bestimme den Punkt algebraisch. (Ausgaben in $) 1‘200 1‘000 800 600 400 200 (Tage) 0 1 2 3 4 5 6 7 Aufgabe 25 Heidi und Leon sind Geschwister. Am 5. Juli beginnt Heidi ihre Ferien in Rimini (Badeort in Italien). Es ist heiss und sie gibt jeden Tag vier Euros für Glacés aus. Leon reist vier Tage später nach Rimini. Er gibt in den folgenden Tagen sechs Euro pro Tag für Glacés aus. An welchem Tag haben die beiden gleich viel Geld für ihre Gelati ausgegeben? Löse die Aufgabe wie folgt: a) b) c) d) e) f) g) Zeichne die beiden Graphen. Bestimme die Funktionsgleichungen. Setze yHeidi yLeon. Löse die entstandene Gleichung auf. Bestimme y. Gib den Schnittpunkt an. Notiere einen Satz. Euro 60 50 40 30 20 10 0 2 4 6 8 10 12 14 Anzahl Glacés Aufgabe 26 Ein gleichschenkliges Dreieck hat einen Umfang von 79 cm. Die beiden Schenkel sind je 5 cm länger als die Basis. Berechne die Länge der Schenkel und die Länge der Basis. Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 56 Aufgabe 27 Von einem Rechteck mit Umfang 90 cm weiss man, dass die Breite 6 cm kürzer als die Länge ist. Berechne die Länge und die Breite. Aufgabe 28 In einem griechischen Restaurant wurden «Meatballs with Leeks» und «Lamb with Yoghurt in the Oven» insgesamt 24 Mal konsumiert. Die Gesamteinnahmen für diese beiden Mahlzeiten betrugen 198 Euro. Wie viele «Meatballs with Leeks» wurden bestellt? Aufgabe 29 Eine Firma besitzt insgesamt 18 Fahrzeuge mit total 82 Rädern. Nebst einigen gewöhlichen Autos gehören auch ein paar Lieferwagen mit je 6 Rädern dazu. Berechne die Anzahl der verschiedenen Fahrzeuge. Aufgabe 30 Auto benötigt pro 100 km 3 Benzin mehr als Auto B. Zusammen verbrauchen sie 16.6 pro 100 km. Wie viel Benzin brauchen die Autos pro 100 km? Aufgabe 31 In einem grossen Sack hat es viermal so viele Marronis wie in einem kleinen. Der Gewichtsunterschied der beiden Säcke beträgt 36 kg. Wie schwer ist der kleinere Sack? Aufgabe 32 Du bist mit einem Schlauchboot auf dem Linthkanal unterwegs. Wenn du ruderst, stellst du mit dem GPS fest, dass du mit der Strömung 4.75 m/s und gegen die Strömung 2.5 m/s erreichst. Wie schnell bewegt sich das Wasser? Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 57 Aufgabe 33 Die rund einen Hektar grosse Masoala-Halle im Zoo Zürich bildet ein Stück des madagassischen Masoala-Regenwaldes ab und beherbergt 45 verschiedene Tierarten und über 3500 Individuen aus Madagaskar, u.a. seltene Bernier-Enten und Alaotra-Bambuslemuren. Von den letztgenannten Arten leben insgesamt 64 Tiere in der Halle, die zusammengerechnet 182 Beine haben. Wie viele Bernier-Enten und Alaotra-Bambuslemuren bevölkern die Masoala-Halle? Aufgabe 34 Wenn bei einer Treppe mit 36 Stufen jede Stufe um 1.8 cm erhöht würde, könnten 4 Stufen eingespart werden. Berechne die Höhe einer Stufe und die der ganzen Treppe. Aufgabe 35 Das Cup-Heimspiel des FC Basel gegen den BSC Young Boys wurde von 24‘465 Fussballfans besucht. Die Einnahmen aus den Zuschauereintritten betrugen 1‘174‘182 Franken. Die anwesenden Jugendlichen bezahlten 25 Fr. Eintritt, die Erwachsenen im Schnitt 56 Fr. Wie viele Jugendliche und Erwachsene besuchten das Spiel? Aufgabe 36 Addiert man 17 zum Elffachen einer Zahl, so ergibt sich dasselbe, wie wenn man das Neunfache dieser Zahl um 4 verkleinert. Wie heisst die Zahl? Aufgabe 37 Die Firma Müller stellte im zweiten Quartal des Jahres aufgrund technischer Probleme sechs grosse Textilmaschinen pro Monat weniger her als in den ersten drei Monaten des Jahres. Wie viele Maschinen wurden im ersten Quartal produziert, wenn im ersten Halbjahr insgesamt 420 Maschinen gebaut wurden. Didacfactory Realschule Buchental Lizenz M3.2620260 Mathematik LU 19: Lineare Funktionen und Gleichungssysteme 58 Aufgabe 38 Der Preis einer Hose wurde um 24.50 CHF reduziert, danach um weitere 15 herabgesetzt. Nun kostet die Hose nur noch die Hälfte des ursprünglichen Preises. Berechne den damaligen und heutigen Preis der Hose. Aufgabe 39 Auf dem Parkplatz der Oberstufe Wier stehen 69 Fahrzeuge. Viele Lehrpersonen kommen von auswärts und pendeln mit ihrem Auto. Die Schüler/innen kommen zu Fuss, mit dem Velo und vereinzelt mit dem Mofa zur Schule. a) Wie viele Autos stehen auf dem Parkplatz, wenn der Hauswart insgesamt 180 Räder zählt? b) Es stehen zudem dreimal so viele Velos wie Mofas beim Veloständer. Wie viele Mofas stehen beim Veloständer? Aufgabe 40 Bestimme zuerst algebraisch und dann grafisch die Schnittpunkte der Geraden und h: a) g1 mit den Punkten A(–1/5) und B(5/5) 5 h1 mit der Funktionsgleichung – 3 3 b) g2 mit der Funktionsgleichung 2 4 4 h2 mit der Funktionsgleichung – – 2 9 1 1 Didacfactory Realschule Buchental Lizenz M3.2620260