Arbeitsblatt: Dossier Flächen und Volumen

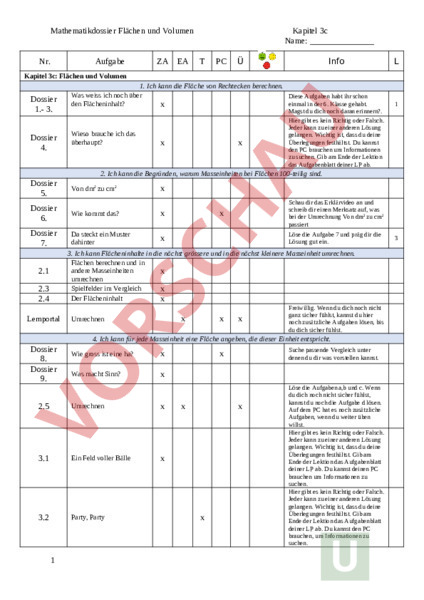
Mathematikdossier Flächen und Volumen Nr. Aufgabe ZA EA Kapitel 3c Name: PC Ü Info Kapitel 3c: Flächen und Volumen Dossier 1.- 3. Dossier 4. 1. Ich kann die Fläche von Rechtecken berechnen. Was weiss ich noch über Diese Aufgaben habt ihr schon einmal in der 6. Klasse gehabt. den Flächeninhalt? Wieso brauche ich das überhaupt? 1 Magst du dich noch daran erinnern?. Hier gibt es kein Richtig oder Falsch. Jeder kann zu einer anderen Lösung gelangen. Wichtig ist, dass du deine Überlegungen festhältst. Du kannst den PC brauchen um Informationen zu suchen. Gib am Ende der Lektion das Aufgabenblatt deiner LP ab. 2. Ich kann die Begründen, warum Masseinheiten bei Flächen 100-teilig sind. Dossier 5. Von dm2 zu cm2 Dossier 6. Wie kommt das? Dossier 7. Da steckt ein Muster dahinter Schau dir das Erklärvideo an und schreib dir einen Merksatz auf, was bei der Umrechnung Von dm2 zu cm2 passiert Löse die Aufgabe 7 und präg dir die Lösung gut ein. 3. Ich kann Flächeninhalte in die nächst grössere und in die nächst kleinere Masseinheit umrechnen. Flächen berechnen und in andere Masseinheiten umrechnen Spielfelder im Vergleich Der Flächeninhalt 2.1 2.3 2.4 Lernportal Umrechnen Freiwillig. Wenn du dich noch nicht ganz sicher fühlst, kannst du hier noch zusätzliche Aufgaben lösen, bis du dich sicher fühlst. 4. Ich kann für jede Masseinheit eine Fläche angeben, die dieser Einheit entspricht. Dossier 8. Dossier 9. Wie gross ist eine ha? Was macht Sinn? 2.5 Umrechnen 3.1 Ein Feld voller Bälle 3.2 Party, Party 1 Suche passende Vergleich unter denen du dir was vorstellen kannst. Löse die Aufgaben a,b und c. Wenn du dich noch nicht sicher fühlst, kannst du noch die Aufgabe lösen. Auf dem PC hat es noch zusätzliche Aufgaben, wenn du weiter üben willst. Hier gibt es kein Richtig oder Falsch. Jeder kann zu einer anderen Lösung gelangen. Wichtig ist, dass du deine Überlegungen festhältst. Gib am Ende der Lektion das Aufgabenblatt deiner LP ab. Du kannst deinen PC brauchen um Informationen zu suchen. Hier gibt es kein Richtig oder Falsch. Jeder kann zu einer anderen Lösung gelangen. Wichtig ist, dass du deine Überlegungen festhältst. Gib am Ende der Lektion das Aufgabenblatt deiner LP ab. Du kannst den PC brauchen, um Informationen zu suchen. 3 Mathematikdossier Flächen und Volumen Kapitel 3c Name: Von den Längenmassen zu den Raummassen 5. Ich kann mit Volumen rechnen und Masseinheiten für den Rauminhalt nennen. Dossier 10. Eisgekühlte Limonade Hier gibt es kein Richtig oder Falsch. Jeder kann zu einer anderen Lösung gelangen. Wichtig ist, dass du deine Überlegungen festhältst. Gib am Ende der Lektion das Aufgabenblatt deiner LP ab. Du kannst den PC brauchen um Informationen zu suchen. 6. Ich kann begründen, warum Masseinheiten bei Raummassen 1000-teilig sind. Dossier 11. Dossier 12. Dossier 13. Dossier 14. Schätzen Umrechnen 4 Schau dir das Erklärvideo an und halte das wichtigste für dich fest. Nicht immer das gleiche Schau dir das Video an, wenn du dir nicht ganz sicher bist. Wenn es klar ist, kannst du weitermachen. Der Spezialfall 7. Ich kann Raummasse in die nächst grössere und in die nächst kleinere Masseinheit umrechnen 5.1 Löse die Aufgaben a-c. Wenn du dir noch nicht ganz sicher bist, löse auch noch die Aufgabe Umrechnen 8. Ich kann die Beziehung zwischen Liter und Kubikdezimeter aufzeigen und die Beziehung zwischen Milliliter in Kubikzentimeter aufzeigen. Dossier Wieviel passt den nun in einen Würfel? 15. Dossier 16. 6.1 Lernportal Beziehungen fürs Leben Präg dir die Beziehung gut ein. Die musst du im Schlaf aufsagen können. Gleich mal probieren Löse die Aufgaben. Dieser Punkt ist freiwillig. Wenn du dich noch nicht ganz sicher fühlst, kannst du hier noch zusätzliche Umrechnungsaufgaben lösen, bis du dich sicher fühlst. Weiter üben 6. Ich kann Raum- in Hohlmasse umrechnen und umgekehrt Dossier 17. Dossier 18. Ein Hotel-Pool Hier kannst du selber probieren. Wenn du hilfe brauchst, kannst du das Video Hotel Pool schauen. Zeig selber was du kannst Orientiere dich an der Aufgabe 17 im Dossier. Hier kannst du selber probieren. Wenn du hilfe brauchst, kannst du das Video Hotel Pool halbvoll schauen. Dossier 19. Wassermangel wegen Klimaerwärmung Dossier 20. Zeig selber was du kannst Das grösste und das kleinste 7.1 Dossier 21. Ab in die Wanne FK Üben formative Lernkontrolle 2 6 Orientiere dich an Aufgabe 19 im Dossier. Hier gibt es kein Richtig oder Falsch. Jeder kann zu einer anderen Lösung gelangen. Wichtig ist, dass du deine Überlegungen festhältst. Du kannst den PC brauchen um Informationen zu suchen. Gib am Ende der Lektion das Aufgabenblatt deiner LP ab. 12 Mathematikdossier Flächen und Volumen Summative LK: 3 Tage im Voraus ankünden. 3 Kapitel 3c Name: Mathematikdossier Flächen und Volumen Kapitel 3c Name: Flächenmasse 1. Nicht nur in der Mathematik wird viel mit den Grössen cm2 (Quadratzentimeter), m2 (Quadratmeter) oder km2 (Quadratkilometer) gerechnet. Ist dir einer der Begriffe auch schon einmal in deinem Alltag begegnet? Wenn ja wo? 2. Vervollständige den Satz: Ein Quadratzentimeter (cm2) beschreibt ein Quadrat mit den Seitenlängen von Zeichne die Fläche auf: 3. Wie gross ist die Fläche von diesem Rechteck? 5 cm 8 cm 4 Mathematikdossier Flächen und Volumen 4. Kapitel 3c Name: Du willst die Wände sowie die Decke deines Zimmers neu streichen. 1.Wie gross ist die gesamte Fläche? Tipp: Nutze andere Gegenstände, um die Länge und Höhe und Länge deiner Wand abzuschätzen. 2. Wie viel Farbe brauchst du? 5 Mathematikdossier Flächen und Volumen 5. Kapitel 3c Name: Das Quadrat hat eine Seitenlänge von 1 dm (cm). Das heisst der Flächeninhalt des Quadrats beträgt dm2. Schätze wie gross ist die Fläche, wenn du sie in cm2 angibst? Meine Schätzung: Überprüfe nun deine Schätzung: Zeichen nun Quadrate mit dem Flächeninhalt von 1 cm2 Seitenlängen ein (Seitenlänge des Quadrats:cm). Wie viele solche Quadrate passen hinein? Stimmt das Resultat mit deiner Schätzung überein? 6. Wieso ist das so? Schau dir das Video 1 an. Was hast du herausgefunden bezüglich des Umrechnens von dm2 in cm2? Notiere dir deine Erkenntnis in einen Merksatz: 6 Mathematikdossier Flächen und Volumen 7. Das schöne an Mathematik ist ihr logischer Aufbau. Es herrschen immer die gleichen Regeln. 1 Are entspricht dabei einer Fläche von 10m mal 10m und eine Hektare entspricht 100m mal 100m. Wie muss dementsprechend die Tabelle aussehen? Was kommt in das Kästchen über dem Pfeil? 1 km2 1 ha 1a 1 m2 1 dm2 1 cm2 8. ha (Hektaren) (Aaren) m2 dm2 100 cm2 mm2 Wie gross ist denn nun 1 a, 1 ha oder 1 km2? Das ist gar nicht so einfach sich vorzustellen. Ergänze die Tabelle so, dass du dir was unter den Grössen vorstellen kannst: 1 dm2 m2 1a ha km2 9. Kapitel 3c Name: Die Handfläche eines erwachsenen Menschen Fläche des Torraums im Fussball Welche Masseinheit macht Sinn, wenn es darum geht die Grössen von folgenden Objekten anzugeben. Schreibpapier Wohnräume Schrebergärten Wiesland bei Bauernhöfen Länder in in in in in Von den Längenmassen zu den Raummassen Wie viel Benzin passt in einem Tank, wie viel Wasser in einem Bassin? Wie viel Medizin 7 Mathematikdossier Flächen und Volumen Kapitel 3c Name: ist in der Flasche? Wie viel Platz hat es im Lagerraum? Bei solchen Fragen geht es um das Volumen, also um die Grösse des Inhalts eines Gefässes oder eines Raumes. Bei Flüssigkeiten verwendet man dazu meist die Hohlmasse, bei anderen stehen die Raummasse im Vordergrund. 10 Du planst im Juni ein Sommerfest. Es haben schon sehr viele Gäste zugesagt. Da es sehr heiss sein wird, überlegst du dir, wie du die Getränke kühlhalten kannst. Da hast du die Idee, die Badewanne mit Eiswürfel zu füllen, so dass du die Flaschen reinstellen kannst. Wie viele Eiswürfel musst du kaufen, damit die Badewanne voll wird, damit die Getränke auch den ganzen Tag schön kühl sind? Tipp: Wie gross ist eine Badewanne? Welche Masse hat ein Eiswürfel? 11 Wieviel cm3 passen in einen dm3? Gib eine Schätzung. Denke dabei an das, was wir schon bei den Flächen gelernt haben. Begründe deine Antwort. Meine Schätzung:_ 8 Eigene Begründung: Mathematikdossier Flächen und Volumen Kapitel 3c Name: 12 Schau dir das Video 2 Volumen an. Halte in eigenen Worten fest, wie die Umrechnung bei Volumen zwischen zwei Masseinheiten funktioniert und weshalb es sich dabei um den Faktor handelt. 13 Und auch hier behält die Mathematik ihren logischen Aufbau bei. Wie muss dementsprechend die Tabelle dieses mal aussehen? Pass auf bei der m3 zu km3! 14 1 cm3 1 dm3 1 m3 mm3 cm3 dm3 1 km3 m3 Weshalb ist die Umrechnung von km3 zu m3 anders? Erkläre zuerst selber. Schau anschliessend das Video 3 von km3 zu m3. Wenn es unterschiede gab, ergänze die Erklärung Eigene Erklärung: 9 Mathematikdossier Flächen und Volumen Kapitel 3c Name: Erklärung im Video: 15 In der Einleitung hast du gelesen, dass man um die Grösse eines Raumes gerne das Raummass wissen will. Bei Flüssigkeiten will man jedoch das Hohlmass wissen. Das heisst, wieviel Flüssigkeit in ein Gefäss oder Raum passen. Dann gibt man die Grösse nicht in cm3 oderm3 an, sondern in ml, cl, oder hl. Beantworte die folgenden beiden Fragen dazu. 1. Gib 3 Beispiele an, wo man die Grösse eines Behälters in ml, cl, dl, oder hl angiebt. 2. Was schätzt du wie lang müssen die Kantenlängen eines Würfels sein, damit genau 1 Litter hinein passen? Beschrifte den Würfel. 16 Damit es nicht zu kompliziert wird, haben die Mathematiker uns da eine einfache Eselsbrücke geschaffen: 1 dm3 1 1 cm3 1 ml 10 Mathematikdossier Flächen und Volumen Kapitel 3c Name: Präg dir dieses Verhältniss gut ein. Anhand dieser Werte kannst du nun alle Hohlmasse in Raummasse umrechnen oder umgekehrt. Perfekt, dass du schon zwischen mm3 und cm3 hin und her rechnen kannst! 17 So nun versuchen wir das ganze einmal anzuwenden. Es gibt zwei Möglichkeiten. Entweder versuchst du die Aufgabe alleine zu lösen, oder du schaust dir das Erklär Video Hotel Pool an. Du darfst entscheiden. Ein Hotel-Pool ist 3m breit und 10m lang. Er ist 2m tief. Wieviel Liter Wasser muss man hineinlaufen lassen, damit er ganz gefüllt ist? 18 11 Wie viel Liter Wasser enthält ein Pool mit den Massen 11m 3m 2.5m? Mathematikdossier Flächen und Volumen Kapitel 3c Name: 19 Der Sommer ist sehr heiss und das Wasser ist knapp geworden. Deshalb kann der Pool aus der Aufgabe 17 nun nur mit 46500 Wasser gefüllt werden. Wie hoch steht das Wasser? Auch hier kannst du entweder erst einmal selber probieren oder gleich das Video Hotel Pool halbvoll anschauen. 20 Wenn du das Video gebraucht hast, probier doch noch diese Aufgabe: Beim zweiten Pool mit den Massen 10 x 3 x 2.5 werden 6600 Wasser eingefüllt. Wie hoch steht das Wasser im Pool? 21 Stell dir vor, alle bewohner des Kanton Zugs genehmigen sich einmal am Tag ein Bad. Das benötigte Wasser würde man vom Zugersee nehmen. Wie lange müsste man das machen, bis der Zugersee ganz leer ist? 12 Mathematikdossier Flächen und Volumen 13 Kapitel 3c Name: