Arbeitsblatt: Test Lineare Funktionen
Material-Details
test
Mathematik
Proportionalität / Prozentrechnen
9. Schuljahr
4 Seiten
Statistik
195716
854
7
19.11.2020
Autor/in
Erika Kaufmann
Land: Schweiz
Registriert vor 2006
Textauszüge aus dem Inhalt:
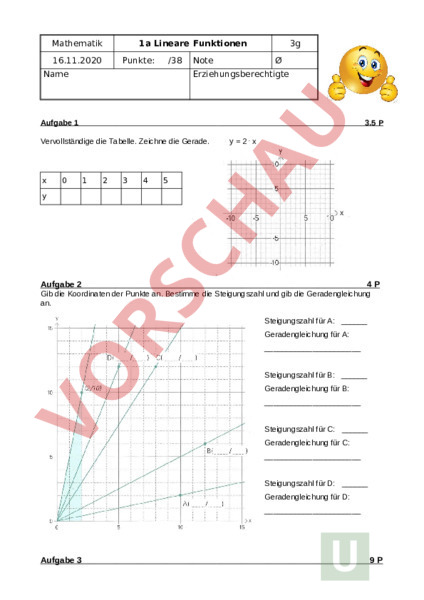
Mathematik 16.11.2020 1a Lineare Funktionen Punkte: /38 Name Note 3g Ø Erziehungsberechtigte Aufgabe 1 3.5 Vervollständige die Tabelle. Zeichne die Gerade. 0 1 2 3 4 y2.x 5 Aufgabe 2 4P Gib die Koordinaten der Punkte an. Bestimme die Steigungszahl und gib die Geradengleichung an. Steigungszahl für A: Geradengleichung für A: Steigungszahl für B: Geradengleichung für B: Steigungszahl für C: Geradengleichung für C: Steigungszahl für D: Geradengleichung für D: Aufgabe 3 9P Vervollständige die Tabellen und zeichne die folgenden Geraden ein. Rot: 3x -5 0 6 12 Blau: 2x 3 0 -1 2 -2 Grün: yx–5 0 -3 3 10 Aufgabe 4 4 Bestimme jeweils die Geradengleichung. Aufgabe 5 Eine Flasche Orangensaft kostet 0.50 Fr. 5P Gib die Funktionsgleichung an, fülle die Tabelle aus und zeichne den Graphen (Achsen beschriften!!). Funktionsgleichung: Aufgabe 6 4P Schreinerei Julen berechnet für die Anfahrt jeweils 40 CHF. Für jede weitere Arbeitsstunde werden 60 CHF berechnet. a) Beschrifte das Koordinatensystem so: auf der x-Achse die Dauer von 0h bis 10h und auf der y-Achse die Kosten von 0 CHF bis 500 CHF. b) Zeichne die Gerade ein. c) Bestimme die Geradengleichung. d) Der Arbeiter muss bei Familie Perren 5 Stunden arbeiten. Wie viel muss die Familie im Total bezahlen? Aufgabe 7 In A, und sind verschiedene Bewegungsabläufe dargestellt. 1.5 Ordne den Beschreibungen je einen Graphen (A, oder C) zu: Ursula wird von der Schule nach Hause geschickt um ein Heft zu holen. Ferdis Rucksack fällt auf seinem Schulweg vom Fahrrad. Anita kauft sich auf dem Weg zur Arbeit in einer Bäckerei ein Pausenbrot Aufgabe 8 8P Wie viel kostet eine Fahrt von 10km in den 4 Städten? Welche Bedeutung hat die Steigung der Geraden für den Tarif? Notiere die Geradengleichung für Taxi C. Die geraden und beginnen nicht bei (0/0). Warum nicht? Beschreibe den Taxitarif, der mit der Geraden gezeigt wird. Was kann man über zwei Taxitarife sagen, deren Geraden parallel verlaufen? Ein Taxi startet eine Aktion, um Kunden anzulocken. Wenn man mindestens 15km weit fährt, sind die ersten 5 km gratis. Anschliessend zahlt man CHF 4 pro km. Zeichne die Gerade ein.