Arbeitsblatt: Leitprogramm Potenzen

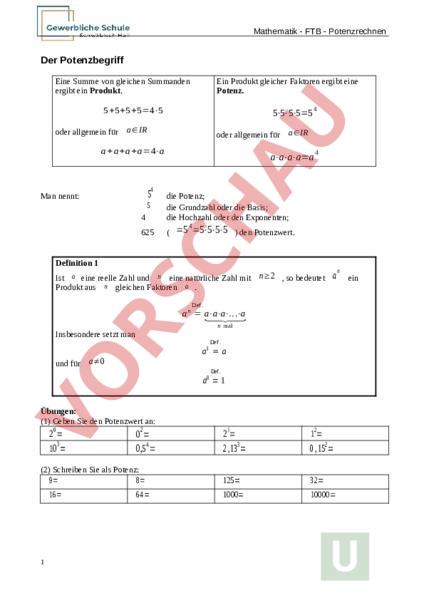
Mathematik FTB Potenzrechnen Der Potenzbegriff Eine Summe von gleichen Summanden ergibt ein Produkt. Ein Produkt gleicher Faktoren ergibt eine Potenz. 555545 55555 oder allgemein für a IR oder allgemein für a IR a aa a4a 4 5 Man nennt: 4 aaaaa 4 die Potenz; die Grundzahl oder die Basis; die Hochzahl oder den Exponenten; 625 5 4 5 4 5555 den Potenzwert. Definition 1 Ist eine reelle Zahl und eine natürliche Zahl mit n2 so bedeutet Produkt aus gleichen Faktoren . an ein Def. aaa .a mal Insbesondere setzt man 1 Def a und für a0 Def. a0 1 Übungen: (1) Geben Sie den Potenzwert an: 20 103 02 0,54 21 12 2,133 0,152 (2) Schreiben Sie als Potenz: 1 9 8 125 32 16 64 1000 10000 Mathematik FTB Potenzrechnen Potenzen mit negativen Zahlen als Exponenten Definition 2 Es ist eine reelle Zahl mit a0 bedeutet an ein Produkt aus und eine natürliche Zahl. Gemäß Definition 1 gleichen Faktoren . Für den negativen Exponenten n wird festgesetzt: Def an In Worten: n ist der Kehrwert von 1 1 1 1 1 . a a a mal . Bemerkung: Damit sind Potenzen für Exponenten aus der Menge der ganzen Zahlen {.,3,2,1,0,1,2,3,.} definiert. Regeln für das Rechnen mit Potenzen Potenzgesetze Es sind und reelle Zahlen und , P1: P2: P3: P4: P5: (In P2 ist a0 in P5 ist b0 .) ganze Zahlen. namanm an anm a a )m anm n a b ( ab) an n b bn () Bemerkungen: (1) Die Potenzgesetze P1-P3 kann man sich verbal merken: Zu P1: Potenzen gleicher Basis werden multipliziert, indem man ihre Exponenten addiert und die Basis beibehält. Zu P2: Potenzen gleicher Basis werden dividiert, indem man ihre Exponenten subtrahiert und die Basis beibehält. Zu P3: Potenzen gleicher Basis werden potenziert, indem man ihre Exponenten multipliziert und die Basis beibehält. Zusammenfassung: Rechenoperationen mit Potenzen gleicher Basis werden ausgeführt, indem man mit den Exponenten die nächst niedrigere Rechenoperation ausführt und die Basis beibehält. Operation zwischen Potenzen cdot 2 Operation im Exponenten „–„ Mathematik FTB Potenzrechnen cdot „hoch (2) Auch die Potenzregeln P4 und P5 kann man sich verbal merken: Zu P4: Potenzen mit gleichen Exponenten werden multipliziert, indem man die Basen multipliziert und den Exponenten beibehält. Zu P5: Potenzen mit gleichen Exponenten werden dividiert, indem man die Basen dividiert und den Exponenten beibehält. (3) Bei den Potenzregeln P4 und P5 handelt es sich um eine Art „Ausklammern. (34 )5 3 545 (34 )535 45 oder für allgemeines und oder für allgemeines (ab )5a5 a5 Sowohl der erste als auch der zweite Summand wird mit 5 multipliziert; die Ergebnisse werden summiert. Entsprechend: und (ab)5 a 5b 5 Sowohl der erste als auch der zweite Faktor wird mit 5 potenziert; die Ergebnisse werden multipliziert. Entsprechend: (ab )5a5a5 n an n b () Übungen (1) Verändern Sie die folgenden Terme durch Anwendung der Potenzgesetze (möglichst vereinfachen). Nennen Sie das angewandte Potenzgesetz, z.B. P3. Alle vorkommenden Nenner seien nicht null. 1 m (d) a 2 (h) (a) y x0 0 (f) 0 3 (e) (b) x y)n( x )n 1 (c) (g) () (b 4 )2 (2) Vereinfachen Sie die folgenden Bruchterme (vorkommende Nenner seien nicht gleich null). 2 2 a1 3 x2 3 2 3 ax 2 x 2 2 (a) 2 ax 3 x (c) 3 ) 2 2 y (b) x x ; a1 4 6 a3 b5 3 5 6 7 3 4 5 y (d) c Mathematik FTB Potenzrechnen Die Wurzel (Potenzen mit gebrochenen Zahlen als Exponenten) Vorbemerkung: Bei der Gleichung ist diejenige Zahl x b bxa b0 gesucht, die mit multipliziert, die Zahl ist Bei der Gleichung xxa oder oder ergibt. Die gesuchte Zahl 2a sind Zahlen gesucht, die mit sich selbst multipliziert die Zahl Zahlen werden mit dem Wurzelzeichen symbolisiert: x ergeben. Die gesuchten x (die Gleichung besitzt zwei Lösungen). Für die Quadratzahlen a1 ,a4 a9 usw. ist x 11 x 42 x 93 usw Für a2 oder für a3 sind die gesuchten Zahlen in ihrer Dezimaldarstellung unendlich und nichtperiodisch (irrationale Zahlen). Durch die folgenden Vereinbarungen werden die Wurzelzahlen den Potenzen zugeordnet. Definition 3 1 2 Sei eine positive reelle Zahl. Unter der Zahl soll diejenige Zahl verstanden werden, deren Quadrat – zweite Potenz – die Zahl ergibt. Für 1 2 1 2 1 2 1 2 2 () a a a gilt: Allgemein: Sei eine ganze Zahl mir q0 diejenige zahl, deren q-te Potenz Für und eine positive reelle Zahl. Die Zahl ergibt. 1 1 ist 1 q gilt: (a a Bemerkungen: (1) Die obige Definition wäre nicht sinnvoll, wenn die Potenzgesetze für die vorkommenden Potenzen nicht gelten würden. Die Definition wurde gerade so gewählt, daß eine Erweiterung des Potenzbegriffes auf rationale Zahlen als Exponenten die Folge ist. 4 Mathematik FTB Potenzrechnen (2) 1 2 a und 1 2 sind zwei Darstellungen für dieselbe Zahl. Potenzschreibweise, a Wurzelschreibweise Es ist also: 1 2 2 a (Quadratwurzel oder zweite Wurzel aus ) und für q0 1 (q-te Wurzel aus ) (3) Für negative reelle Zahlen sind Wurzeln nicht definiert. Eine Erweiterung der Definitionen in diese Richtung führt zum Begriff der „komplexen Zahlen. Übungen (1) Wenden Sie P1 bzw. P3 an: 1 2 1 q 1 2 (a a q ) q p (2) Zeigen Sie durch Anwendung von Definitionen und Potenzregeln: (3) Schreiben Sie mit Wurzelzeichen und bestimmen Sie den Potenzwert. 1 2 1 3 9 27 0 32 3 4 1 5 3 2 ) ) 2 3 8 3 1 27 9 2 16 ) 1 1 4 16 1 8 3 27 100 1 (4) Vereinfachen sie folgende Wurzelterme. Benennen Sie das jeweils angewandte Potenzgesetz. 3 (a) 3 100 33 3 (b) x 6 3 (c) (5) Zeigen Sie durch Anwendung der Potenzregeln (a) 5 ab ab (b) a a b 3 (d) 2 3 2 a 2 Mathematik FTB Potenzrechnen (6) Vereinfachen Sie: 4 (a) 4 1 4 a: 8 2 7 4 64y 4y 3 6 (b) 3 7 53 2 : 5 5 5 (c) 2 6 x5 x 32 6 (d)