Arbeitsblatt: Repetition

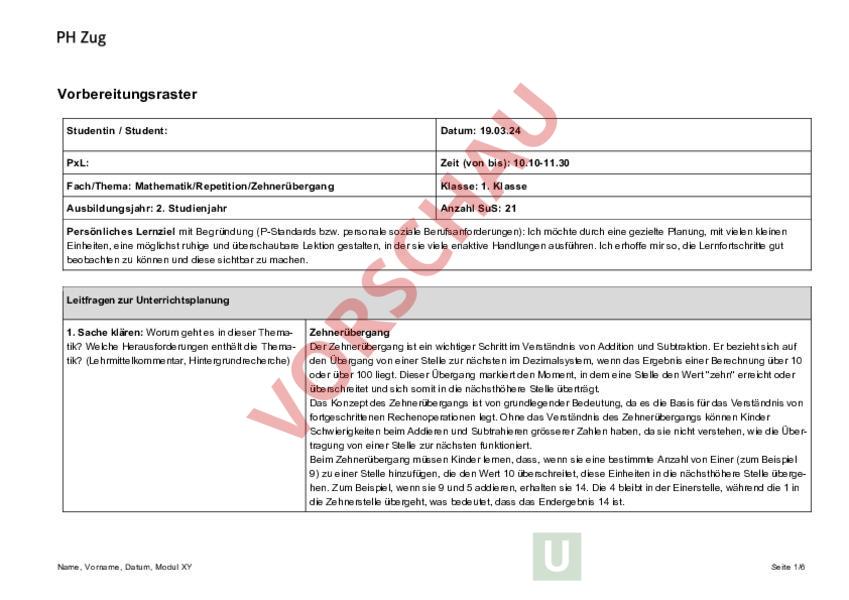
Vorbereitungsraster Studentin Student: Datum: 19.03.24 PxL: Zeit (von bis): 10.10-11.30 Fach/Thema: Mathematik/Repetition/Zehnerübergang Klasse: 1. Klasse Ausbildungsjahr: 2. Studienjahr Anzahl SuS: 21 Persönliches Lernziel mit Begründung (P-Standards bzw. personale soziale Berufsanforderungen): Ich möchte durch eine gezielte Planung, mit vielen kleinen Einheiten, eine möglichst ruhige und überschaubare Lektion gestalten, in der sie viele enaktive Handlungen ausführen. Ich erhoffe mir so, die Lernfortschritte gut beobachten zu können und diese sichtbar zu machen. Leitfragen zur Unterrichtsplanung 1. Sache klären: Worum geht es in dieser Thematik? Welche Herausforderungen enthält die Thematik? (Lehrmittelkommentar, Hintergrundrecherche) Name, Vorname, Datum, Modul XY Zehnerübergang Der Zehnerübergang ist ein wichtiger Schritt im Verständnis von Addition und Subtraktion. Er bezieht sich auf den Übergang von einer Stelle zur nächsten im Dezimalsystem, wenn das Ergebnis einer Berechnung über 10 oder über 100 liegt. Dieser Übergang markiert den Moment, in dem eine Stelle den Wert zehn erreicht oder überschreitet und sich somit in die nächsthöhere Stelle überträgt. Das Konzept des Zehnerübergangs ist von grundlegender Bedeutung, da es die Basis für das Verständnis von fortgeschrittenen Rechenoperationen legt. Ohne das Verständnis des Zehnerübergangs können Kinder Schwierigkeiten beim Addieren und Subtrahieren grösserer Zahlen haben, da sie nicht verstehen, wie die Übertragung von einer Stelle zur nächsten funktioniert. Beim Zehnerübergang müssen Kinder lernen, dass, wenn sie eine bestimmte Anzahl von Einer (zum Beispiel 9) zu einer Stelle hinzufügen, die den Wert 10 überschreitet, diese Einheiten in die nächsthöhere Stelle übergehen. Zum Beispiel, wenn sie 9 und 5 addieren, erhalten sie 14. Die 4 bleibt in der Einerstelle, während die 1 in die Zehnerstelle übergeht, was bedeutet, dass das Endergebnis 14 ist. Seite 1/6 Das Verständnis des Zehnerübergangs ist auch wichtig für das Verständnis von Dezimalzahlen, Brüchen und anderen fortgeschrittenen mathematischen Konzepten. Es ermöglicht den Schülern, eine solide Basis für das Verständnis von Rechenoperationen und den Umgang mit Zahlen im Allgemeinen aufzubauen. (Pikas 2. Bedingungen klären: Über welche Erfahrungen (welches Vorwissen) verfügen die Kinder? Die Schüler und Schülerinnen befinden sich im Aufbau von Plusrechnungen. Sie können relativ sicher bis zwanzig zählen und erste Plusrechnungen durchführen. Einige haben jedoch noch Schwierigkeiten, vom zählenden Rechnen wegzukommen, während andere dies problemlos können. Um die SuS sicherer im Umgang mit Additionen zu machen, dient die Lektion zur Übung des Zehnerübergangs, um sie danach weiter voranzubringen. Vorwissen: Zahlen bis 20, Verdoppeln/Halbieren ,10er Freunde, Zerlegen 3. Konsequenzen für die Gestaltung: Wie organisiere ich das Lernen? Wie gestalte ich die Differenzierung? Dank des Team-Teachings können auch die schwächeren SuS unterstützt werden. Die Aufgaben im Zahlenbuch sind ausserdem oft differenziert gestaltet. Es stehen immer Zwanzigerpunktefelder zur Verfügung sowie Materialien, um die SuS aktiv an die Aufgaben heranzuführen. Zwischendurch finden auch Spiele statt, bei denen einerseits Bewegung entsteht und andererseits der Zehnerübergang spielerisch geübt werden kann. Die Einführung der Themen erfolgt im Kreis, mit allen Kindern gleichzeitig. 4. Fachliche Kompetenzen: nach Lehrplan 21 MA.1.C.1a Die SuS können zeigen, wie sie zählen. MA.1.C.1b Die SuS können Summen darstellen und Darstellungen nachvollziehen (z.B. auf dem 20er-Feld oder auf dem Zahlenstrahl). MA.1.A.2.1b Die SuS können können im Zahlenraum bis 20 von beliebigen Zahlen aus vorwärts und rückwärts zählen. Die SuS können in 2er-Schritten vorwärts zählen, von 2 bis 20. Die SuS können Fingerbilder von 1 bis 10 spontan zeigen sowie Anzahlen bis 5 ohne Zählen erfassen. Name, Vorname, Datum, Modul XY Seite 2/6 4a) Minimale Lernziele Die SuS zeigen anhand verschiedener Übungen, dass sie das Konzept des verdoppeln und der Verliebten Zahlen verstanden haben. 4b) Erweiterte Lernziele Die SuS wenden Strategien beim Zehnerübergang an (Kein zählendes Rechnen). 5. Überfachliche Kompetenz (personale, methodische oder soziale) nach LP 21 Methodische Kompetenzen: Die SuS können bekannte Muster hinter der Aufgabe/dem Problem erkennen und daraus einen Lösungsweg ableiten. Verlaufsplanung Zeit 10 Didaktische Begründung Aktivitäten Lehrperson Aktivitäten SuS • • • • Lernprozesse organisieren, anleiten und begleiten Arbeitsaufträge, Moderation Lerntätigkeiten (z.B. zuhören, Informationen suchen, experimentieren, Lernaufgabe bearbeiten) LP leitet verschiedene Spiele im Kreis an und führt diese durch. Die SuS hören und schauen zu. Lernprozessphasen Aufgabentypen Didakt. Modelle, Theoriebezüge Teilziele Medien Sozialformen Spielblätter Ganze Gruppe Einstieg/Konfrontation Verschiedene Zählspiele zur Repetition des Zahlverständnisses anhand verschiedener Darstellungsformen (gesprochenes Zahlwort und gezeigtes Fingerbild, zählen nach akustischen Reizen). Name, Vorname, Datum, Modul XY Die SuS beteiligen sich aktiv. AA: Ich erkläre oder zeige die Spielregeln und danach spielen wir gemeinsam. Seite 3/6 Spiele: Zahlensport, Zahlen hören, In Schritten zählen (Pikas, Mathekartei). Diese Aktivitäten dienen zur Aktivierung des Vorwissens aber auch dem Automatisieren des bereits gelernten Stoffes. 10 Erarbeitung Zahl und Operationsverständnis und Zahlzerlegung AA: Ich verteile euch allen ein Kärtchen. Ihr Die SuS betrachten ihr Bild und überlegen. sollt nun herausfinden welches Kind zu euch Die SuS suchen den passenden Partner. gehört, findet euren Partner. Übung Partner finden, die Darstellungsvernetzung wird geübt. F: Wieso gehört ihr zusammen? Partnerarbeit: Wieviel fehlt bis zur 10? 30 Zahldarstellungskarten Tandem Die SuS spielen gemeinsam das Spiel. AA: Zu zweit zeigt ihr abwechselnd Fingerzahlbilder. Das andere Kind ergänzt auf zehn. Übungsaufgabe 5 Posten zum Repetieren verschiedener Kompetenzen wie Zahlzerlegung, Verdoppeln und einfache Plusaufgaben mit Zehnerübergang (Halli Galli, Memory, Brettspiel, Wurfspiel). Name, Vorname, Datum, Modul XY LP zeigt die einzelnen Posten vor und erklärt die Regeln. AA: Jede Gruppe kommt an allen Posten vorbei. Wechsel erfolgt im 5 Minuten Takt. Die SuS schauen zu und stellen Fragen. Die SuS arbeiten an den verschiedenen Posten. Die SuS hören einander zu. Diverse ViererSpielmate- gruppen rialien wie Spielpläne, Glocke, Karten usw. Seite 4/6 5-10 Ganze Gruppe Reflexion Die Reflexion dient der Quali- F: Was hat euch gefallen, was weniger? tätssicherung und der Klärung eventueller Fragen, sowie der F: Gibt es Fragen, noch Unsicherheiten? Planung für die nächsten Lektionen. Wir tauschen uns darüber aus was gut funktioniert hat. Es ist auch wichtig, dass wir eventuelle Fehler korrigieren und sicherstellen, dass alle Schülerinnen und Schüler das Material richtig verstanden haben. 10 Abschluss Arbeitsblatt zum Thema Zeh- LP zeigt am Visualizer die zu bearbeitenden nerübergang. Es dient der Er- Aufgaben Schritt für Schritt vor. fassung des Lernstands in schriftlicher Form und kann zusätzlich genutzt werden, um die verbleibende Zeit sinnvoll zu nutzen. Es ermöglicht den Schülerinnen und Schülern, ihre Fähigkeiten im Zehnerübergang zu üben und zu vertiefen, während gleichzeitig Name, Vorname, Datum, Modul XY Die SuS folgen der Erklärung und stellen Fragen bei Unsicherheiten. AB Einzelarbeit Die SuS bearbeiten das Arbeitsblatt. Seite 5/6 ihr Fortschritt dokumentiert wird. à Arbeitsaufträge und-anweisungen (AA) (s. Skript UL 1, Kapitel 7.4 „Arbeitsaufträge und -anweisungen erteilen) sowie Fragen (F) und Impulse (I) (s. Skript UL 1, Kapitel 6.2.2 „Mit Fragen und Impulsen anregen) werden ausformuliert und fett geschrieben. Version: August 2021 Name, Vorname, Datum, Modul XY Seite 6/6