Arbeitsblatt: Kurztheorie Volumen Oberfläche

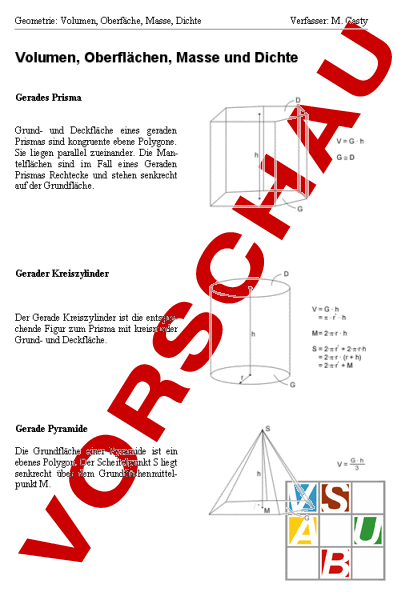
Geometrie: Volumen, Oberfäche, Masse, Dichte Verfasser: M. Casty Volumen, Oberflächen, Masse und Dichte Gerades Prisma Grund- und Deckfläche eines geraden Prismas sind kongruente ebene Polygone. Sie liegen parallel zueinander. Die Mantelflächen sind im Fall eines Geraden Prismas Rechtecke und stehen senkrecht auf der Grundfläche. Gerader Kreiszylinder Der Gerade Kreiszylinder ist die entsprechende Figur zum Prisma mit kreisrunder Grund- und Deckfläche. Gerade Pyramide Die Grundfläche einer Pyramide ist ein ebenes Polygon. Der Scheitelpunkt liegt senkrecht über dem Grundflächenmittelpunkt M. 1/2 Geometrie: Volumen, Oberfäche, Masse, Dichte Verfasser: M. Casty Gerader Kreiskegel Der Gerade Kreiskegel ist die entsprechende Figur zur Pyramide mit kreisrunder Grundfläche. Kugel Für die Berechnung von Oberfläche und Volumen von Kugeln braucht man nur deren Radius zu kennen. Wie schon beim Kreis spielt auch hier die Kreiszahl (3.1415) eine wichtige Rolle. 1) Dichte und Masse Die Dichte ist definiert als Masse pro Volumeneinheit. Die Dichte wird in der Einheit kg/m3 (kg pro m3) gemessen. Die Dichte eines Stoffes gibt an, wie viel Masse dieses Stoffes in einem Kubikmeter platz findet. Man könnte sie also als Mass bezeichnen, welches angibt, wie dicht gepackt ein Stoff wie beispielsweise Gold oder Wasser ist. Sie lässt sich als Stoffeigenschaft verstehen. Zahlwerte für die Dichte sind Tabellen zu entnehmen oder müssen in der Aufgabenstellung angegeben sein. V daraus erhält man: V 2/2 ; m·V