Arbeitsblatt: Spezielle Punktmengen im Dreieck

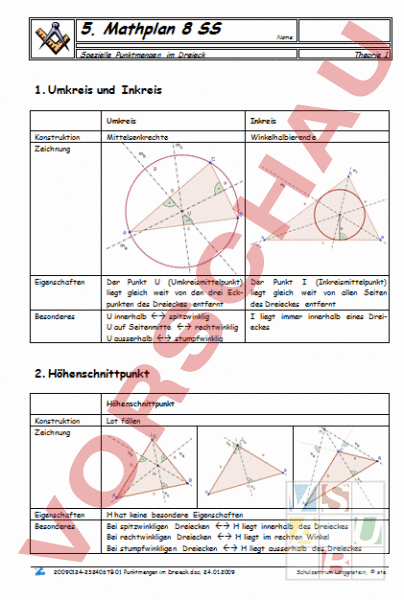
5. Mathplan 8 SS Name: Spezielle Punktmengen im Dreieck Theorie 1 1. Umkreis und Inkreis Umkreis Inkreis Konstruktion Zeichnung Mittelsenkrechte Winkelhalbierende Eigenschaften Der Punkt (Umkreismittelpunkt) liegt gleich weit von den drei Eckpunkten des Dreieckes entfernt innerhalb spitzwinklig auf Seitenmitte rechtwinklig ausserhalb stumpfwinklig Der Punkt (Inkreismittelpunkt) liegt gleich weit von allen Seiten des Dreieckes entfernt liegt immer innerhalb eines Dreieckes Besonderes 2. Höhenschnittpunkt Höhenschnittpunkt Konstruktion Zeichnung Lot fällen Eigenschaften Besonderes hat keine besondere Eigenschaften Bei spitzwinkligen Dreiecken liegt innerhalb des Dreieckes Bei rechtwinkligen Dreiecken liegt im rechten Winkel Bei stumpfwinkligen Dreiecken liegt ausserhalb des Dreieckes 20090124-232406TB 01 Punktmengen im Dreieck.doc; 24.01.2009 Schulzentrum Längenstein, ste Mathematik 8 SS Theorie 3. Schwerpunkt Eine weitere spezielle Punktmenge ist der Schwerpunkt. Jedes Dreieck besitzt einen Schwerpunkt. Er liegt in jedem Falle innerhalb des Dreieckes. Wir konstruieren die Seitenhalbierenden des Dreieckes. Schwerpunkt Konstruktion Zeichnung Besonderes Eigenschaften 20090124-232406TB 01 Punktmengen im Dreieck.doc; 24.01.2009 Schulzentrum Längenstein, ste Mathematik 8 SS Theorie 4. Mitteldreieck Mitteldreieck Konstruktion Zeichnung Eigenschaften 20090124-232406TB 01 Punktmengen im Dreieck.doc; 24.01.2009 Schulzentrum Längenstein, ste Mathematik 8 SS Theorie 5. Die Eulergerade Wir konstruieren den Umkreismittelpunkt, den Höhenschnittpunkt und den Schwerpunkt eines Dreieckes. Wir achten dabei, dass wir sehr genau und sehr fein konstruieren. Wir erkennen, dass 20090124-232406TB 01 Punktmengen im Dreieck.doc; 24.01.2009 Schulzentrum Längenstein, ste