Arbeitsblatt: Es muss nicht immer 10 sein!

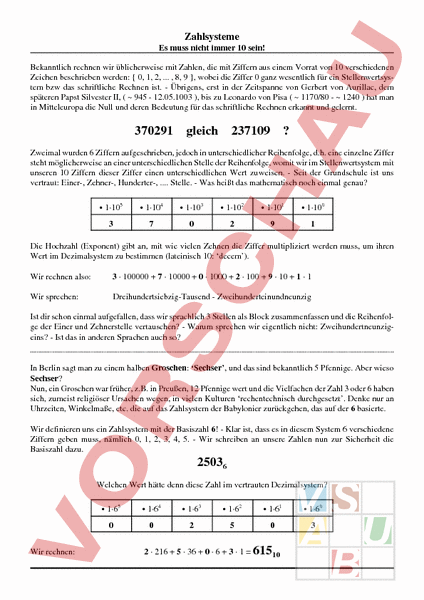
Zahlsysteme Es muss nicht immer 10 sein! Bekanntlich rechnen wir üblicherweise mit Zahlen, die mit Ziffern aus einem Vorrat von 10 verschiedenen Zeichen beschrieben werden: 0, 1, 2, . 8, 9 }, wobei die Ziffer 0 ganz wesentlich für ein Stellenwertsystem bzw das schriftliche Rechnen ist. Übrigens, erst in der Zeitspanne von Gerbert von Aurillac, dem späteren Papst Silvester II, 945 12.05.1003 ), bis zu Leonardo von Pisa 1170/80 1240 hat man in Mitteleuropa die Null und deren Bedeutung für das schriftliche Rechnen erkannt und gelernt. 370291 gleich 237109 Zweimal wurden 6 Ziffern aufgeschrieben, jedoch in unterschiedlicher Reihenfolge, d.h. eine einzelne Ziffer steht möglicherweise an einer unterschiedlichen Stelle der Reihenfolge, womit wir im Stellenwertsystem mit unseren 10 Ziffern dieser Ziffer einen unterschiedlichen Wert zuweisen. Seit der Grundschule ist uns vertraut: Einer-, Zehner-, Hunderter-, Stelle. Was heißt das mathematisch noch einmal genau? 1·105 1·104 1·103 1·102 1·101 1·100 3 7 0 2 9 1 Die Hochzahl (Exponent) gibt an, mit wie vielen Zehnen die Ziffer multipliziert werden muss, um ihren Wert im Dezimalsystem zu bestimmen (lateinisch 10: ‘decem). Wir rechnen also: 3 · 100000 7 · 10000 0 · 1000 2 · 100 9 · 10 1 · 1 Wir sprechen: Dreihundertsiebzig-Tausend Zweihunderteinundneunzig Ist dir schon einmal aufgefallen, dass wir sprachlich 3 Stellen als Block zusammenfassen und die Reihenfolge der Einer und Zehnerstelle vertauschen? Warum sprechen wir eigentlich nicht: Zweihundertneunzigeins? Ist das in anderen Sprachen auch so? In Berlin sagt man zu einem halben Groschen: ‘Sechser, und das sind bekanntlich 5 Pfennige. Aber wieso Sechser? Nun, ein Groschen war früher, z.B. in Preußen, 12 Pfennige wert und die Vielfachen der Zahl 3 oder 6 haben sich, zumeist religiöser Ursachen wegen, in vielen Kulturen ‘rechentechnisch durchgesetzt. Denke nur an Uhrzeiten, Winkelmaße, etc. die auf das Zahlsystem der Babylonier zurückgehen, das auf der 6 basierte. Wir definieren uns ein Zahlsystem mit der Basiszahl 6! Klar ist, dass es in diesem System 6 verschiedene Ziffern geben muss, nämlich 0, 1, 2, 3, 4, 5. Wir schreiben an unsere Zahlen nun zur Sicherheit die Basiszahl dazu. 25036 Welchen Wert hätte denn diese Zahl im vertrauten Dezimalsystem? Wir rechnen: 1·65 1·64 1·63 1·62 1·61 1·60 0 0 2 5 0 3 2 · 216 5 · 36 0 · 6 3 · 1 61510 Zahlsysteme Es muss nicht immer 10 sein! Das Verfahren muss ja wohl mit jeder (natürlichen) Basiszahl größer als 1 klappen, man muss nur einen entsprechenden Zeichenvorrat haben. Wir versuchen es mit der kleinsten Möglichkeit, mit der Basiszahl 2. Im Dualsystem gibt es nur die Ziffern 0 und 1. 1101012 Welchen Wert hätte denn diese Zahl im vertrauten Dezimalsystem? Wir rechnen: 1·25 1·24 1·23 1·22 1·21 1·20 1 1 0 1 0 1 1 · 32 1 · 16 0 · 8 1 · 4 0 · 2 1 · 1 5310 Wird die Basiszahl größer als 10, so muss man sich weitere Ziffern definieren. Es ist üblich, für die Ziffer 10 den Buchstaben A, die Ziffer 11 den Buchstaben B, . die Ziffer 15 den Buchstaben F, usw zu schreiben. Aufgaben: a) Bestimme den Wert im Dezimalsystem: 31546, 31548, 315412 - Warum ist die Zahl 31544 nicht sinnvoll? b) Bestimme den Wert im Dezimalsystem: ABBA12, ABBA16, FF16, CAD14, 11011101102, 47118 Wie rechnet man nun am einfachsten Dezimalzahlen in andere Zahlsysteme um? Man könnte sich sicher den dezimalen Wert der einzelnen Stellen merken und entsprechend probieren, mit zulässigen Vervielfachungen aufzufüllen, wie das folgende Beispiel einer Umwandlung von 11710 in das Dualsystem zeigt. Die Stelle mit sieben Zweien (27 128) ist zu groß, aber 26 64 wird sicher benötigt. Nimmt man 25 32 dazu, so ist man bei 96 angelangt, was noch zu klein ist. Nimmt man noch 24 16 dazu, so ist man bei 112 angelangt, was immer noch zu klein ist. Bestätige: 1 · 64 1 · 32 1 · 16 0 · 8 1 · 4 0 · 2 1 · 1 11710 11101012 Geht das nicht auch systematisch? Nun, ein Stellenwertsystem ist so aufgebaut, dass von Stelle zu Stelle jeweils ein Faktor der Basiszahl dazu kommt. Wenn wir nun die Umkehroperation der Multiplikation, die Division, ganzzahlig durchführen was ergibt sich? 370291 10 37029 Rest 1 (in der letzten Stelle war keine 10 ‘enthalten) 37029 10 3702 Rest 9 (in der vorletzten Stelle war eine 10 ‘enthalten) 3702 10 370 Rest 2 (die 2 stand auf der Hunderterstelle mit zwei mal einer 10!) usw. Zahlsysteme Es muss nicht immer 10 sein! 4711 Das ist gar nicht schwer! Als Oktalzahl (Basiszahl 8): Probe: 4711 588 73 9 1 : : 8 8 8 8 8 588 Rest 7 73 Rest 4 9 Rest 1 1 Rest 1 0 Rest 1 1 · 4096 1 · 512 1 · 64 4 · 8 7 · 1 471110 111478 Als Dualzahl (Basiszahl 2): 4711 2355 1177 588 294 147 73 36 18 9 4 2 1 : : : : : : 2 2 2 2 2 2 2 2 2 2 2 2 2 2355 1177 588 294 147 73 36 18 9 4 2 1 0 Rest Rest Rest Rest Rest Rest Rest Rest Rest Rest Rest Rest Rest 1 1 1 0 0 1 1 0 0 1 0 0 1 471110 10010011001112 Wenn man bedenkt, dass jede 8 aus 3 Zweien besteht, kann man dann die Oktalziffern in der Dualzahldarstellung erkennen? Aufgabe: Wandele 471110 in die Systeme mit der Basiszahl 6 und 16 um! Dualzahlen können ganz schön lang werden, allerdings hat dieses Zahlsystem den Vorteil, dass es nur zwei Ziffern gibt, was sich technisch leicht durch 2 verschiedene ‘Zustände (Licht an Licht aus; Spannung keine Spannung; langer Ton kurzer Ton; Loch kein Loch; magnetisch nicht magnetisch; etc) realisieren läßt. Deshalb ein kurzer Exkurs in die Informationstechnologie! Ein Bit ist ein Speicherbaustein, der die zwei Zustände 0 und 1 annehmen kann. Dieses Kunstwort kommt von: binary digit, was mathematisch eine Ziffer im Dualsystem beschreibt. Für die Zusammenfassung von 8 Bits hat man das Wort: Byte geprägt, das heißt, dass mathematisch 1 Byte eine 8-stellige Dualzahl ist.1 Die größte Zahl, die man demnach mit einem Byte darstellen kann ist demnach: 111111112 Was ist dieser Wert als Dezimalzahl? Verstehst Du nun, warum ein Zeichensatz beim Computer gewöhnlich aus 256 Zeichen besteht, wobei der alte, amerikanische Standard-Code für den Informationsaustausch (American Standard Code for Information Interchange abgekürzt: ASCII) nur 7 Bit verwendete, weil das 1 Besonderheit: 1 KB (ein KiloByte) sind nicht 1000 (Kilo) Byte sondern 210 1024 Byte. Zahlsysteme Es muss nicht immer 10 sein! erste Bit des Byte als Steuerzeichen benutzt wurde?! Weil nun Dualzahlen leicht sehr viele Stellen aufweisen, hat man (nicht nur in der Informationstechnologie) vereinbart, in einem Zahlsystem zu rechnen, das kürzere Zahldarstellungen, und damit eine größere Basiszahl verwendet. In der technischen Realisierung hat man vereinbart, ein halbes Byte als Ziffer zu nehmen, das heißt in diesem Zahlsystem gibt es die Ziffern: 00002 11112, das sind sechzehn verschiedene Ziffern! Damit ist es klar: Das abgeleitete Zahlsystem, mit dem viele Computer arbeiten ist mathematisch das Zahlsystem mit der Basiszahl 16 (Sedezimalsystem alt: Hexadezimalsystem). Die Ziffern, die durch ein halbes Byte repräsentiert werden, sind 0, 1, 2, , D, E, F! Aufgaben: 1) In der ASCII-Tabelle werden die großen Buchstaben dezimal, beginnend mit A, von 65 ab dargestellt, die kleinen Buchstaben kommen 32 Stellen später, der kleine Buchstabe entspräche dezimal 97. Gib für das Wort: a l (a) den aus 4 Dezimalzahlen, (b) den aus 4 Dualzahlen, (c) den aus 4 Sedezimalzahlen bestehenden Code gemäß ASCII-Tabelle an. 2) Geheimschrift: Vereinbare mit deinem Nachbarn ein Zahlsystem und die Stellenanzahl für den Zahlcode jedes Buchstabens. Nun denkt sich jeder eine kurze, vertrauliche Nachricht aus. Codiert die Nachricht mit Hilfe der ASCII-Tabelle in euer Zahlsystem und tauscht aus! Decodiere die Nachricht des Nachbarn (nicht schummeln!) Rechnen mit Dualzahlen Unsere Welt ist zunehmend digital geprägt, nahezu Alles läßt sich einer Folge von Ziffern aus 0 1 beschreiben. Kann man mit Dualzahlen eigentlich auch rechnen wie gewohnt? Ausprobieren:2 Addition: Subtraktion: Multiplikation: Division: 110111100 10011010 1111000 1001110 101101 · 101 101010000 11000 Gib jeweils die zugehörige Rechnung in Dezimalzahlen an und vergleiche die Ergebnisse Stimmt es? Überprüfe deine Rechentechnik an jeweils einem weiteren (selbstgewählten) Beispiel! Bei deinen Beispielen kann natürlich bei der Subtraktion und der Division ein kleines Problem aufgetaucht 2 Schreibe, wie gewohnt, stellenweise untereinander (bzw rechne im Päckchen). Beachte Überträge bzw wann man etwas borgen muß und der multiplikative Unterschied im Wert benachbarter Stellen ist 2! Zahlsysteme Es muss nicht immer 10 sein! sein! Es ist z.B. bei der Division zu vermuten, dass das Ergebnis nicht aufgeht. Was ist zu tun? Dualzahlen mit Nachkommastellen: 101,1101 Vergleichen wir wieder mit unseren Vereinbarungen im Stellenwertsystem bei Dezimalzahlen, so ist darunter zu verstehen: 1·40·21·11·1 1·1 0·1 1· 1 2 4 8 16 Bestätige, dass hier (dezimal) 5,8125 dargestellt wurde. Da in der Bruchdarstellung im Nenner nur der Primfaktor 2 auftauchen kann, ist der Bruch, mit einer geeigneten Anzahl von Primfaktoren 5 immer so zu erweitern, dass die zugehörige Dezimaldarstellung endlich ist! Subtraktion durch Komplementbildung: Eine letzte rechentechnische Besonderheit soll nun noch dargestellt werden. Subtraktionsaufgaben lassen sich (durch geeignetes Borgen) auf die Addition zurückführen. Zuerst ein Beispiel aus dem Dezimalsystem: 1) 864 517 864 ( 1000 517 - 1000 864 483 (- 1000) (1)347 2) 864 517 864 ( 999 517 1 1000 864 482 1 (- 1000) (1)347 Die geborgten 1000 gibt man nach der Addition einfach wieder zurück; aber warum im 2. Fall so kompliziert (999 1)? Sieh dir die Ziffern der Subtraktionsaufgabe (517) und der Additionsaufgabe (482) an was ergibt sich stets bei der Summe der Ziffern auf den entsprechenden Stellen?! Was bedeutet dieses Verfahren im Dualsystem? 11011 10110 11011 (11111 10110) 1 100000 11011 01001 1 (- 100000) (1)00101 Richtig! Die Ziffern-Schalter werden einfach umgedreht, dann addiert, geborgte Stelle auf Null gesetzt! So einfach kann Subtraktion sein! Übrigens, welche Rechnung wurde denn da oben dual eigentlich ausgeführt? Aufgabe: Rechne dual mit Komplementbildung: 57 39