Arbeitsblatt: Prüfung Proportionalität und umgekehrte Proportionalität

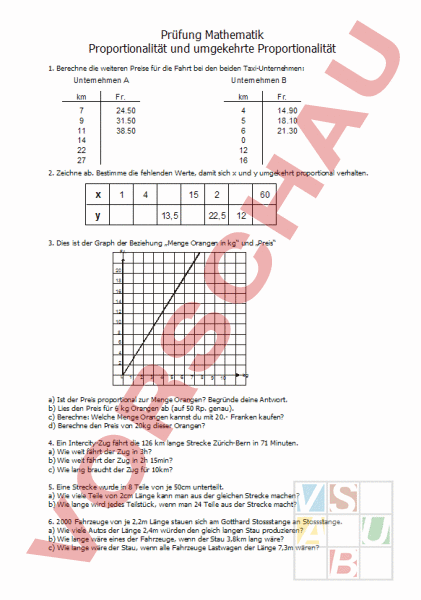
Prüfung Mathematik Proportionalität und umgekehrte Proportionalität 1. Berechne die weiteren Preise für die Fahrt bei den beiden Taxi-Unternehmen: Unternehmen Unternehmen km Fr. km Fr. 7 9 11 14 22 27 24.50 31.50 38.50 4 5 6 0 12 16 14.90 18.10 21.30 2. Zeichne ab. Bestimme die fehlenden Werte, damit sich und umgekehrt proportional verhalten. 1 4 15 2 13,5 60 22,5 12 3. Dies ist der Graph der Beziehung „Menge Orangen in kg und „Preis Fr. 20 18 16 14 12 10 8 6 4 2 0 1 2 3 4 5 6 7 8 9 10 kg a) Ist der Preis proportional zur Menge Orangen? Begründe deine Antwort. b) Lies den Preis für 6 kg Orangen ab (auf 50 Rp. genau). c) Berechne: Welche Menge Orangen kannst du mit 20.- Franken kaufen? d) Berechne den Preis von 20kg dieser Orangen? 4. Ein Intercity-Zug fährt die 126 km lange Strecke Zürich-Bern in 71 Minuten. a) Wie weit fährt der Zug in 3h? b) Wie weit fährt der Zug in 2h 15min? c) Wie lang braucht der Zug für 10km? 5. Eine Strecke wurde in 8 Teile von je 50cm unterteilt. a) Wie viele Teile von 2cm Länge kann man aus der gleichen Strecke machen? b) Wie lange wird jedes Teilstück, wenn man 24 Teile aus der Strecke macht? 6. 2000 Fahrzeuge von je 2,2m Länge stauen sich am Gotthard Stossstange an Stossstange. a) Wie viele Autos der Länge 2,4m würden den gleich langen Stau produzieren? b) Wie lange wäre eines der Fahrzeuge, wenn der Stau 3,8km lang wäre? c) Wie lange wäre der Stau, wenn alle Fahrzeuge Lastwagen der Länge 7,3m wären?