Arbeitsblatt: Satz des Pythagoras

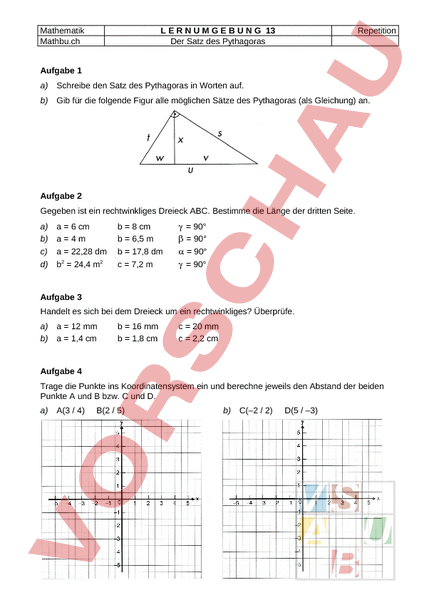
Mathematik Mathbu.ch E N M E U G 13 Der Satz des Pythagoras Repetition Aufgabe 1 a) Schreibe den Satz des Pythagoras in Worten auf. b) Gib für die folgende Figur alle möglichen Sätze des Pythagoras (als Gleichung) an. Aufgabe 2 Gegeben ist ein rechtwinkliges Dreieck ABC. Bestimme die Länge der dritten Seite. a) b) c) d) 6 cm a4m 22,28 dm b2 24,4 m2 8 cm 6,5 b 17,8 dm 7,2 90 90 90 90 Aufgabe 3 Handelt es sich bei dem Dreieck um ein rechtwinkliges? Überprüfe. a) b) 12 mm 1,4 cm 16 mm 1,8 cm 20 mm 2,2 cm Aufgabe 4 Trage die Punkte ins Koordinatensystem ein und berechne jeweils den Abstand der beiden Punkte und bzw. und D. a) A(3 4) B(2 5) b) C(–2 2) D(5 –3) Mathematik Mathbu.ch E N M E U G 13 Der Satz des Pythagoras Repetition Aufgabe 5 Ein Feuerwehrauto steht in 12 Entfernung von einem brennenden Haus. Die Drehleiter auf dem Dach des Feuerwehrwagens (Höhe 3,20 m) wird 24 ausgefahren. Welche Höhe erreicht die Leiter an der Hauswand? (Tipp: Mache eine Skizze!) Aufgabe 6 Berechne den Flächeninhalt des Rechtecks. Aufgabe 7 Ein gleichseitiges Dreieck hat eine Seitenlänge von 20 cm. Berechne den Flächeninhalt des Dreiecks. (Tipp: Fertige eine Skizze an!) Aufgabe 8 Bestimme die Dachfläche des Turmdachs (Dachhöhe hk 6 m), das aus vier deckungsgleichen gleichschenkligen Dreiecken besteht (Grundseite 8 m). Aufgabe 9 Ist es möglich, eine 6,30 lange und 2,15 breite rechteckige Tischblatte durch eine 2,10 hohe und 90 cm breite Tür zu transportieren? Beweise. Aufgabe 10 Wie tief ist der Graben? Mathematik Mathbu.ch E N M E U G 13 Der Satz des Pythagoras Repetition Lösung Aufgabe 1 a) In allen rechtwinkligen Dreiecken ist die Summe der beiden Kathetenquadrate gleich dem Hypotenusequadrat. b) 2 s 2 t2 t2 w2 x2 s2 v2 x2 Aufgabe 2 Gegeben ist ein rechtwinkliges Dreieck ABC. Bestimme die Länge der dritten Seite. a) b) c) d) 6 cm a4m 22,28 dm b2 24,4 m2 8 cm 6,5 b 17,8 dm 7,2 90 90 90 90 10 cm 5,12 c 13,4 dm 4,94 5,24 Aufgabe 3 Handelt es sich bei dem Dreieck um ein rechtwinkliges? Überprüfe. a) b) 12 mm 1,4 cm 16 mm 1,8 cm ja, weil 122 162 202 nein, weil 1,42 1,82 2,22 20 mm 2,2 cm Aufgabe 4 Trage die Punkte ins Koordinatensystem ein und berechne jeweils den Abstand der beiden Punkte und bzw. und D. a) A(3 4) B(2 5) b) B• 1 C(–2 2) D(5 –3) 2 1 •A C• 7 74 5 •D Abstand 2 1,41 Abstand 74 8,6 Lösung Mathematik Mathbu.ch E N M E U G 13 Der Satz des Pythagoras Repetition Aufgabe 5 Ein Feuerwehrauto steht in 12 Entfernung von einem brennenden Haus. Die Drehleiter auf dem Dach des Feuerwehrwagens (Höhe 3,20 m) wird 24 ausgefahren. Welche Höhe erreicht die Leiter an der Hauswand? (Tipp: Mache eine Skizze!) Die Leiter erreicht eine Höhe von 23,98 Aufgabe 6 Berechne den Flächeninhalt des Rechtecks. 66,14 A 4960,78 m2 Aufgabe 7 Ein gleichseitiges Dreieck hat eine Seitenlänge von 20 cm. Berechne den Flächeninhalt des Dreiecks. (Tipp: Fertige eine Skizze an!) 17,32 cm 173,20 cm2 Aufgabe 8 Bestimme die Dachfläche des Turmdachs (Dachhöhe hk 6 m), das aus vier deckungsgleichen gleichschenkligen Dreiecken besteht (Grundseite 8 m). 2 2 8m 2 (6 m)2 ( 2 hs2 hk2 ( hs2 hs2 7,21 h a 4· 2 4· 4,21 8 2 115, 36 m2 Aufgabe 9 Ist es möglich, eine 6,30 lange und 2,15 breite rechteckige Tischblatte durch eine 2,10 hohe und 90 cm breite Tür zu transportieren? Beweise. Ja, es ist möglich (Diagonale der Türe 2,28 m). Aufgabe 10 Wie tief ist der Graben? Der Graben ist 2,45 tief.