Arbeitsblatt: Kreisteile berechnen

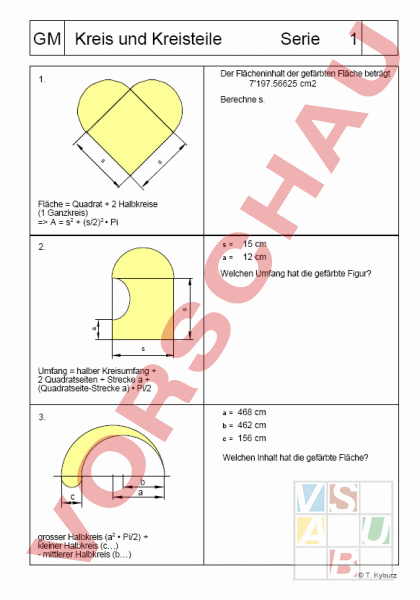
GM Kreis und Kreisteile Serie 1 Der Flächeninhalt der gefärbten Fläche beträgt 7197.56625 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 15 cm 12 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 3. 468 cm 462 cm 156 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 1 184 cm 46 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 70.8 cm Die Kathete misst die Kathete ist 94.4 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 22 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 1 Der Umfang der gefärbten Fläche beträgt 76.59 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 12.5 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 9 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 2 Der Flächeninhalt der gefärbten Fläche beträgt 33297.221985 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 528 cm 208 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 6430 3. cm 216 cm 103 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 2 58 cm 18 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 708.4 cm Die Kathete misst die Kathete ist 2669.6 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 403 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 2 Der Umfang der gefärbten Fläche beträgt 527.21 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 776.5 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 12 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 3 Der Flächeninhalt der gefärbten Fläche beträgt 201.02414 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 572 cm 436 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 6590 3. cm 3 cm 80 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 3 317 cm 50 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 3351.3 cm Die Kathete misst die Kathete ist 2517.9 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 623 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 3 Der Umfang der gefärbten Fläche beträgt 640.38 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 922.5 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 15 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 4 Der Flächeninhalt der gefärbten Fläche beträgt 43554.868525 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 534 cm 312 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 7613 3. cm 266 cm 146 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 4 598 cm 92 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 3434.8 cm Die Kathete misst die Kathete ist 4026.4 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 191 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 4 Der Umfang der gefärbten Fläche beträgt 85.47 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 438.3 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 60 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 5 Der Flächeninhalt der gefärbten Fläche beträgt 3344.514495 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 583 cm 99 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 1351 3. cm 331 cm 138 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 5 862 cm 84 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 3779.0 cm Die Kathete misst die Kathete ist 2083.5 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 379 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 5 Der Umfang der gefärbten Fläche beträgt 494.75 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 221.3 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 22 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 6 Der Flächeninhalt der gefärbten Fläche beträgt 27485.00662 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 810 cm 382 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 9045 3. cm 86 cm 86 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 6 456 cm 31 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 5998.9 cm Die Kathete misst die Kathete ist 1795.5 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 318 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 6 Der Umfang der gefärbten Fläche beträgt 676.20 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 941.5 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 45 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 7 Der Flächeninhalt der gefärbten Fläche beträgt 715.9221 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 650 cm 232 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 9222 3. cm 310 cm 111 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 7 816 cm 3 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 2103.9 cm Die Kathete misst die Kathete ist 252.2 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 674 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 7 Der Umfang der gefärbten Fläche beträgt 649.95 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 646.5 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 66 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 8 Der Flächeninhalt der gefärbten Fläche beträgt 34460.34558 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 501 cm 480 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 3742 3. cm 301 cm 49 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 8 561 cm 58 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 1587.4 cm Die Kathete misst die Kathete ist 4900.4 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 211 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 8 Der Umfang der gefärbten Fläche beträgt 172.83 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 749.1 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 48 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 9 Der Flächeninhalt der gefärbten Fläche beträgt 34126.090485 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 144 cm 68 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 2948 3. cm 444 cm 123 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 9 295 cm 16 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 4902.7 cm Die Kathete misst die Kathete ist 4606.6 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 597 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 9 Der Umfang der gefärbten Fläche beträgt 973.58 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 957.4 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 82 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 10 Der Flächeninhalt der gefärbten Fläche beträgt 1984.46628 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 52 cm 148 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 3. 780 cm 297 cm 309 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 10 308 cm 14 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 4760.3 cm Die Kathete misst die Kathete ist 3284.5 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 504 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 10 Der Umfang der gefärbten Fläche beträgt 706.91 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 967.9 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 33 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 11 Der Flächeninhalt der gefärbten Fläche beträgt 31641.97548 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 134 cm 23 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 4184 3. cm 247 cm 56 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 11 772 cm 40 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 6752.8 cm Die Kathete misst die Kathete ist 1892.2 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 375 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 11 Der Umfang der gefärbten Fläche beträgt 317.68 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 306.2 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 77 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 12 Der Flächeninhalt der gefärbten Fläche beträgt 14452.873875 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 189 cm 468 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 9860 3. cm 137 cm 102 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 12 182 cm 3 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 3832.7 cm Die Kathete misst die Kathete ist 3362.6 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 930 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 12 Der Umfang der gefärbten Fläche beträgt 594.95 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 295.5 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 92 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 13 Der Flächeninhalt der gefärbten Fläche beträgt 22166.717575 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 120 cm 165 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 8252 3. cm 442 cm 176 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 13 340 cm 70 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 5821.1 cm Die Kathete misst die Kathete ist 2380.0 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 26 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 13 Der Umfang der gefärbten Fläche beträgt 926.01 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 518.8 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 2 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 14 Der Flächeninhalt der gefärbten Fläche beträgt 43923.55473 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 464 cm 92 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 7692 3. cm 178 cm 23 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 14 804 cm 16 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 5495.8 cm Die Kathete misst die Kathete ist 3927.4 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 333 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 14 Der Umfang der gefärbten Fläche beträgt 74.42 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 758.0 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 97 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 15 Der Flächeninhalt der gefärbten Fläche beträgt 1510.406335 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 708 cm 10 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 9234 3. cm 770 cm 47 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 15 660 cm 84 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 9680.1 cm Die Kathete misst die Kathete ist 1303.9 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 942 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 15 Der Umfang der gefärbten Fläche beträgt 912.80 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 365.1 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 55 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 16 Der Flächeninhalt der gefärbten Fläche beträgt 10802.67865 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 212 cm 84 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 3. 809 cm 563 cm 28 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 16 404 cm 86 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 1654.4 cm Die Kathete misst die Kathete ist 2750.4 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 989 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 16 Der Umfang der gefärbten Fläche beträgt 898.62 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 64.2 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 55 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 17 Der Flächeninhalt der gefärbten Fläche beträgt 24908.686815 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 806 cm 20 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 5216 3. cm 119 cm 36 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 17 207 cm 6 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 8145.6 cm Die Kathete misst die Kathete ist 1429.5 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 70 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 17 Der Umfang der gefärbten Fläche beträgt 132.10 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 233.8 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 69 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 18 Der Flächeninhalt der gefärbten Fläche beträgt 31251.37495 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 837 cm 41 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 8583 3. cm 203 cm 9 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 18 334 cm 16 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 1724.2 cm Die Kathete misst die Kathete ist 3951.1 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 129 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 18 Der Umfang der gefärbten Fläche beträgt 187.87 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 544.7 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 2 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 19 Der Flächeninhalt der gefärbten Fläche beträgt 42922.527365 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 978 cm 9 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 1790 3. cm 231 cm 8 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 19 776 cm 44 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 432.2 cm Die Kathete misst die Kathete ist 1654.0 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 773 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 19 Der Umfang der gefärbten Fläche beträgt 222.24 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 179.4 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 74 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 20 Der Flächeninhalt der gefärbten Fläche beträgt 1758.999285 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 270 cm 22 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 3700 3. cm 807 cm 80 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 20 827 cm 55 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 459.0 cm Die Kathete misst die Kathete ist 2378.8 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 906 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 20 Der Umfang der gefärbten Fläche beträgt 225.13 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 697.9 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 92 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 21 Der Flächeninhalt der gefärbten Fläche beträgt 13761.58449 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 819 cm 11 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 5597 3. cm 358 cm 13 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 21 960 cm 65 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 6407.9 cm Die Kathete misst die Kathete ist 4013.4 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 495 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 21 Der Umfang der gefärbten Fläche beträgt 487.42 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 29.9 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 17 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 22 Der Flächeninhalt der gefärbten Fläche beträgt 45309.292335 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 266 cm 70 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 3514 3. cm 708 cm 49 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 22 660 cm 50 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 2895.4 cm Die Kathete misst die Kathete ist 1739.2 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 923 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 22 Der Umfang der gefärbten Fläche beträgt 399.84 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 27.8 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 36 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 23 Der Flächeninhalt der gefärbten Fläche beträgt 43936.785865 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 911 cm 56 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 8725 3. cm 842 cm 31 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 23 397 cm 35 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 388.3 cm Die Kathete misst die Kathete ist 2959.5 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 69 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 23 Der Umfang der gefärbten Fläche beträgt 950.50 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 58.0 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 14 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz GM Kreis und Kreisteile Serie 24 Der Flächeninhalt der gefärbten Fläche beträgt 38429.855435 cm2 1. Berechne s. Fläche Quadrat 2 Halbkreise (1 Ganzkreis) s2 (s/2)2 • Pi 2. 812 cm 65 cm Welchen Umfang hat die gefärbte Figur? Umfang halber Kreisumfang 2 Quadratseiten Strecke (Quadratseite-Strecke a) • Pi/2 4907 3. cm 742 cm 60 cm Welchen Inhalt hat die gefärbte Fläche? a grosser Halbkreis (a2 • Pi/2) kleiner Halbkreis (c) mittlerer Halbkreis (b) T. Kyburz GM Kreis und Kreisteile 4. Serie 24 123 cm 21 cm Welchen Inhalt hat die gefärbte Fläche? Quadrat (s2) 2 grosse Halbkreise (grosser Ganzkreis - 2 kleine Halbkreise (kleiner Ganzkreis mit [s-2a]/2) 7026.1 cm Die Kathete misst die Kathete ist 4046.1 cm lang. Welchen Flächeninhalt haben die beiden «Möndchen» zusammen? 5. Halbkreis über Kathete Halbkreis über Kathete rechtwinkliges Dreieck (a • b/2) Halbkreis über Hypotenuse (Pythagoras!) 6. 240 551 cm Welchen äusseren Umfang hat die Figur aus den drei Kreisteilen? 3 mal 240 720 die drei Bögen sind zusammen so gross wie 2 ganze Umfänge. T. Kyburz GM Kreis und Kreisteile 7. Serie 24 Der Umfang der gefärbten Fläche beträgt 387.31 cm Berechne a. Umfang Viertelskreis 2a • Pi 4 Umfang zwei Halbkreise a/2 • Pi 2 • halbe Quadratseite. Da in der Formel immer gleich gross ist, kann es weggelassen werden, d.h. es wird nur mit den Bruchteilen von Pi gerechnet! 8. 519.0 cm Wie lang sind die drei Kreisbogen? Umfang 2 Halbkreise Umfang Ganzkreis; also 2 • • Pi Umfang Viertelskreis 9. 2 cm Die Seiten des Quadrates messen Berechne den Inhalt der gefärbten Fläche. weisse Fläche Fläche QuadratFläche Viertelskreis T. Kyburz