Arbeitsblatt: Wahrscheinlichkeit Baumdiagramm Theorie

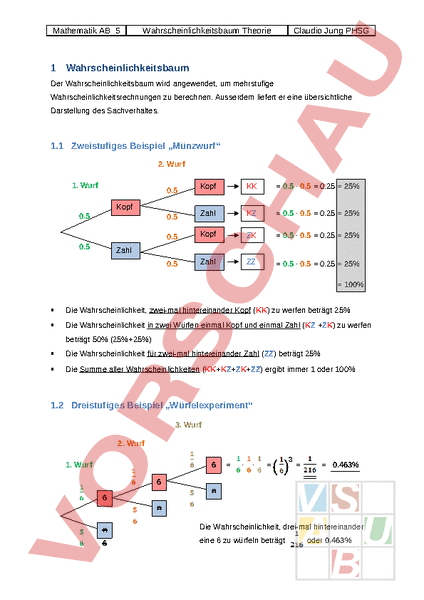
Mathematik AB_5 Wahrscheinlichkeitsbaum Theorie Claudio Jung PHSG 1 Wahrscheinlichkeitsbaum Der Wahrscheinlichkeitsbaum wird angewendet, um mehrstufige Wahrscheinlichkeitsrechnungen zu berechnen. Ausserdem liefert er eine übersichtliche Darstellung des Sachverhaltes. 1.1 Zweistufiges Beispiel „Münzwurf 2. Wurf 1. Wurf Kopf KK 0.5 · 0.5 0.25 25% 0.5 Zahl KZ 0.5 · 0.5 0.25 25% 0.5 Kopf ZK 0.5 · 0.5 0.25 25% 0.5 Zahl ZZ 0.5 · 0.5 0.25 25% 0.5 Kopf 0.5 0.5 Zahl 100% • Die Wahrscheinlichkeit, zwei-mal hintereinander Kopf (KK) zu werfen beträgt 25% • Die Wahrscheinlichkeit in zwei Würfen einmal Kopf und einmal Zahl (KZ ZK) zu werfen beträgt 50% (25%25%) • Die Wahrscheinlichkeit für zwei-mal hintereinander Zahl (ZZ) beträgt 25% • Die Summe aller Wahrscheinlichkeiten (KKKZZKZZ) ergibt immer 1 oder 100% 1.2 Dreistufiges Beispiel „Würfelexperiment 3. Wurf 2. Wurf 1. Wurf 6 · · 3 () 0.463% 6 6 n Die Wahrscheinlichkeit, drei-mal hintereinander 6 eine 6 zu würfeln beträgt oder 0.463% Mathematik AB_5 Wahrscheinlichkeitsbaum Theorie Claudio Jung PHSG 1.3 Ziehen ohne Zurücklegen Wenn ich aus einem Gefäss mit farbigen Kugeln eine Kugel herausnehme und entferne, verändern sich die Wahrscheinlichkeiten gezogen zu werden für die Kugeln, welche noch im Gefäss sind. Beispiel: Ich habe ein Gefäss mit 2 roten und 3 blauen Kugeln, also insgesamt 5 Kugeln. Wie gross ist die Wahrscheinlichkeit, dass ich nacheinander drei blaue Kugeln ziehe? 1. Zug blau Jetzt hat es nur noch 2 blaue und 2 rote Kugeln, also insgesamt 4 Kugeln im Gefäss. rot 2. Zug Jetzt hat es nur noch 1. Zug blau 1 blaue und 2 rote · Kugeln, also blau insgesamt 3 Kugeln rot im Gefäss. rot 3. Zug 2. Zug 1. Zug blau · · blau rot blau rot rot Die Wahrscheinlichkeit, 3 blaue Kugeln nacheinander zu ziehen beträgt oder 10%