Arbeitsblatt: Trigonometrie - Strecken, Stauchen, Verschieben von sin(x)

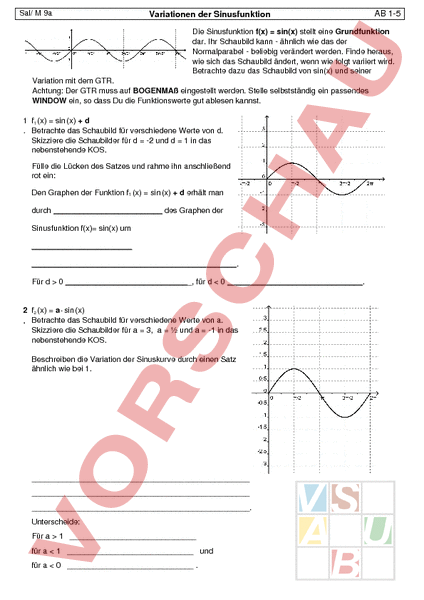
Sal/ 9a Variationen der Sinusfunktion AB 15 Die Sinusfunktion f(x) sin(x) stellt eine Grundfunktion dar. Ihr Schaubild kann ähnlich wie das der Normalparabel beliebig verändert werden. Finde heraus, wie sich das Schaubild ändert, wenn wie folgt variiert wird. Betrachte dazu das Schaubild von sin(x) und seiner Variation mit dem GTR. Achtung: Der GTR muss auf BOGENMAß eingestellt werden. Stelle selbstständig ein passendes WINDOW ein, so dass Du die Funktionswerte gut ablesen kannst. 1 f1 (x) sin (x) d Betrachte das Schaubild für verschiedene Werte von d. Skizziere die Schaubilder für 2 und 1 in das nebenstehende KOS. Fülle die Lücken des Satzes und rahme ihn anschließend rot ein: Den Graphen der Funktion f1 (x) sin (x) d erhält man durch des Graphen der Sinusfunktion f(x) sin(x) um . Für 0, für 0. 2 f2 (x) a sin (x) Betrachte das Schaubild für verschiedene Werte von a. Skizziere die Schaubilder für 3, und 1 in das nebenstehende KOS. Beschreiben die Variation der Sinuskurve durch einen Satz ähnlich wie bei 1. . Unterscheide: Für 1 für 1 und für 0 Sal/ 9a Variationen der Sinusfunktion AB 15 3 Bestimme die Funktionsgleichung folgender Graphen: 4 f3 (x) sin (x – c): Betrachte das Schaubild für verschiedene Werte von c. Skizziere die Schaubilder für und in das nebenstehende 2 KOS. Fülle die Lücken des Satzes und rahme ihn anschließend rot ein: Den Graphen der Funktion f3 (x) sin (x c) erhält man durch des Graphen der Sinusfunktion f(x) sin(x) um . Für 0, für 0 . 5 f4 (x) sin (bx): Betrachte das Schaubild für verschiedene Werte von b. Skizziere die Schaubilder für 2 und in das nebenstehende KOS. Beschreiben die Variation der Sinuskurve durch einen Satz ähnlich wie bei 1. . 6 Fülle die Tabelle aus: Wertebereich (x) sin (x) f1 (x) sin (x) d f2 (x) a sin (x) f3 (x) sin (x – c) f4 (x) sin (b x) Periode Sal/ 9a Variationen der Sinusfunktion 7 Bestimme die Funktionsgleichung folgender Graphen: AB 15